Question

已知关于x的二次函数f（x）=x²+ax-b（a，b∈R）．
（Ⅰ）当b=-2时，由于对任意的x∈R，函数f（x）的值总大于零，求实数a的取值范围；
（Ⅱ）如果方程f（x）=0有一个负根和一个不大于1的正根，求实数a，b满足的条件，并在右图所给坐标系中画出点（a，b）所在的平面区域；
（Ⅲ）在第（Ⅱ）问的条件下，若实数k满足b=k（a+1）+3，求k的取值范围．

Answer 1

分析：（Ⅰ）当b=-2时，f（x）=x²+ax+2，由于对任意的x∈R，函数f（x）的值总大于零，从而其判别式小于0，故可求实数a的取值范围；
（Ⅱ）利用方程f（x）=0有一个负根和一个不大于1的正根，可得

f(0)＜0 f(1)≥0

，从而可表示相应区域．
（Ⅲ）依题意，a≠-1，则k=

b-3

a+1

表示区域内的动点（a，b）与（-1，3）连线的斜率，故可求．

解答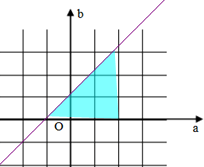：解：（Ⅰ）当b=-2时，f（x）=x²+ax+2，由于对任意的x∈R，函数f（x）的值总大于零，
∴△=a²-8＜0，
∴-2

2

＜a＜2

2

（Ⅱ）∵方程f（x）=0有一个负根和一个不大于1的正根，
∴

f(0)＜0 f(1)≥0

，
∴

b＞0 1+a-b≥0

（Ⅲ）依题意，a≠-1，则k=

b-3

a+1

表示区域内的动点（a，b）与（-1，3）连线的斜率，则k＜1．

点评：本题主要考查方程根的讨论问题及平面区域的确定，同时考查利用线性规划知识解决有关取值问题．