题目内容
已知关于x的二次函数f(x)=ax2-8bx+1.
(1)设集合M={1,2,3}和N={-1,1,2,3,4,5},从集合M中随机取一个数作为a,从N中随机取一个数作为b,求函数y=f(x)在区间[2,+∞)上是增函数的概率;
(2)设点(a,b)是区域
内的随机点,求函数y=f(x)在区间[2,+∞)上是增函数的概率.
(1)设集合M={1,2,3}和N={-1,1,2,3,4,5},从集合M中随机取一个数作为a,从N中随机取一个数作为b,求函数y=f(x)在区间[2,+∞)上是增函数的概率;
(2)设点(a,b)是区域
|
分析:(I)记事件A=“函数y=f(x)在区间上是增函数”,根据二次函数的图象与性质,可得A包含的基本事件需满足a∈M、b∈N且2b≤a,由此可得共有5个基本事件,再由古典概型计算公式即可算出所求的概率.
(II)作出不等式组表示的平面区域,得到△AOC及其内部,其中A(6,0),B(0,6).再由(I)的不等式组解出符合题意的不等式组表示的平面区域为△AOB及其内部,其中B(4,2),由此结合几何概型计算公式即可算出相应的概率.
(II)作出不等式组表示的平面区域,得到△AOC及其内部,其中A(6,0),B(0,6).再由(I)的不等式组解出符合题意的不等式组表示的平面区域为△AOB及其内部,其中B(4,2),由此结合几何概型计算公式即可算出相应的概率.
解答: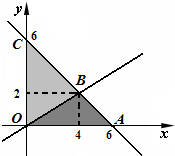 解(Ⅰ)∵函数f(x)=ax2-8bx+1的图象的对称轴为x=
解(Ⅰ)∵函数f(x)=ax2-8bx+1的图象的对称轴为x=
.
∴要使f(x)=ax2-8bx+1在区间[2,+∞)上为增函数,
当且仅当a>0且
≤2,即2b≤a.…2′
由此可得:若a=1,则b=-1;若a=2则b=±1;若a=3,则b=±1.…5′
记事件A=“函数y=f(x)在区间上是增函数”
则事件A包含基本事件的个数是1+2+2=5个
因此,所求事件A的概率为P(A)=
.…7′
(Ⅱ)由(Ⅰ)知当且仅当2b≤a且a>0时,函数f(x)=ax2-8bx+1在区间[2,+∞)上为增函数,
依条件可知试验的全部结果所构成的区域为:
,
对应图中的△AOC及其内部,其中A(6,0),B(0,6)
而构成所求事件的区域为△AOB部分及其内部,如图所示.…9′
由
解得交点为B(4,2).…11′
∴函数在区间[2,+∞)上是增函数的概率为P=
=
=
.…14′.
答:两种情况下,函数y=f(x)在区间[2,+∞)上是增函数的概率分别为
和
.
 解(Ⅰ)∵函数f(x)=ax2-8bx+1的图象的对称轴为x=
解(Ⅰ)∵函数f(x)=ax2-8bx+1的图象的对称轴为x=| 4b |
| a |
∴要使f(x)=ax2-8bx+1在区间[2,+∞)上为增函数,
当且仅当a>0且
| 4b |
| a |
由此可得:若a=1,则b=-1;若a=2则b=±1;若a=3,则b=±1.…5′
记事件A=“函数y=f(x)在区间上是增函数”
则事件A包含基本事件的个数是1+2+2=5个
因此,所求事件A的概率为P(A)=
| 5 |
| 18 |
(Ⅱ)由(Ⅰ)知当且仅当2b≤a且a>0时,函数f(x)=ax2-8bx+1在区间[2,+∞)上为增函数,
依条件可知试验的全部结果所构成的区域为:
|
对应图中的△AOC及其内部,其中A(6,0),B(0,6)
而构成所求事件的区域为△AOB部分及其内部,如图所示.…9′
由
|
∴函数在区间[2,+∞)上是增函数的概率为P=
| S△AOB |
| S△AOC |
| ||
|
| 1 |
| 3 |
答:两种情况下,函数y=f(x)在区间[2,+∞)上是增函数的概率分别为
| 5 |
| 18 |
| 1 |
| 3 |
点评:本题着重考查了二次函数的图象与性质、古典概型和几何概型计算公式,考查了二元一次不等式组表示的平面区域等知识,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 已知关于x的二次函数f(x)=x2+ax-b(a,b∈R).
已知关于x的二次函数f(x)=x2+ax-b(a,b∈R).