题目内容
推理：因为平行四边形对边平行且相等，而矩形是特殊的平行四边形，所以矩形的对边平行且相等．以上推理的方法是（ ）
| A．合情推理 | B．演绎推理 | C．归纳推理 | D．类比推理 |
B
解析试题分析：每个演绎推理部有两个前提，即大前提（概括性的一般原理）和小前提（对个别事物的判断）、根据两个前提之间的关系做出新判断（推理），得出结论。本题中平行四边形对边平行且相等为大前提（概括性的一般原理），矩形是特殊的平行四边形为小前提（对个别事物的判断），根据两个前提之间的关系做出新判断（推理），得出矩形的对边平行且相等，所以本题为演绎推理。选B。
考点：演绎推理及合情推理
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
把正整数按一定的规则排成了如图所示的三角形数表．设
是位于这个三角形数表中从上往下数第
行，从左往右数第
个数，若
，则与的和为( )
| A．105 | B．103 | C．82 | D．81 |
用数学归纳法证明“
时，从“
到
”时，左边应增添的式子是（ ）
A． | B． | C． | D． |
对于任意正整数n，定义“
”如下：
当n是偶数时，
，
当n是奇数时，
现在有如下四个命题：
①
；
②
；
③
的个位数是0；
④
的个位数是5。
其中正确的命题有（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
凡自然数都是整数，而 4是自然数 所以，4是整数。以上三段论推理（ ）
| A．正确 | B．推理形式不正确 |
| C．两个“自然数”概念不一致 | D．两个“整数”概念不一致 |
用反证法证明命题：“若整系数一元二次方程
有有理根，那么
中至少有一个是偶数时，下列假设中正确的是
| A．假设都是偶数 |
| B．假设都不是偶数 |
| C．假设至多有一个是偶数 |
| D．假设至多有两个是偶数 |
的值是
，则输出
的值是 
若a，b∈R，则下面四个式子中恒成立的是( )
| A．lg(1＋a2)>0 | B．a2＋b2≥2(a－b－1) |
| C．a2＋3ab>2b2 | D． < |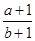
分析法是从要证明的结论出发，逐步寻求使结论成立的（ ）
| A．充分条件 | B．必要条件 | C．充要条件 | D．等价条件 |