[题目]在直角坐标系x0y中.把曲线α为参数)上每个点的横坐标变为原来的倍.纵坐标不变.得到曲线以坐标原点为极点.以x轴正半轴为极轴.建立极坐标系.曲线的极坐标方程(1)写出的普通方程和的直角坐标方程,(2)设点M在上.点N在上.求|MN|的最小值以及此时M的直角坐标. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】在直角坐标系x0y中，把曲线α为参数)上每个点的横坐标变为原来的倍，纵坐标不变，得到曲线以坐标原点为极点，以x轴正半轴为极轴，建立极坐标系，曲线的极坐标方程

（1）写出的普通方程和的直角坐标方程；

（2）设点M在上，点N在上，求|MN|的最小值以及此时M的直角坐标.

【答案】（1）的普通方程为，的直角坐标方程为. （2）最小值为，此时

【解析】

（1）由的参数方程消去求得的普通方程，利用极坐标和直角坐标转化公式，求得的直角坐标方程.

（2）设出点的坐标，利用点到直线的距离公式求得最小值的表达式，结合三角函数的指数求得的最小值以及此时点的坐标.

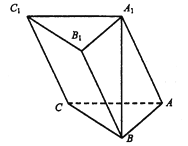
（1）由题意知的参数方程为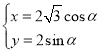（为参数）

所以的普通方程为.由得，所以的直角坐标方程为.

（2）由题意，可设点的直角坐标为，

因为是直线，所以的最小值即为到的距离，

因为．

当且仅当时，取得最小值为，此时的直角坐标为即．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

相关题目

【题目】在平面直角坐标系xOy中，曲线C1的参数方程为（φ为参数），在以O为极点，x轴的正半轴为极轴的极坐标系中，曲线C2是圆心为（2，），半径为1的圆．

（1）求曲线C1的普通方程和C2的直角坐标方程；

（2）设M为曲线C1上的点，N为曲线C2上的点，求|MN|的取值范围．

【题目】如图，在三棱柱中，平面，，且.

（1）求棱与所成的角的大小；

（2）在棱上确定一点，使二面角的平面角的余弦值为.

【题目】现有甲、乙两种不同规格的产品，其质量按测试指标分数进行划分，其中分数不小于分的为合格品，否则为次品.现随机抽取两种产品各件进行检测，其结果如下：

测试指数分数
甲产品
乙产品

（1）根据以上数据，完成下边的列联表，并判断是否有的有把握认为两种产品的质量有明显差异？

	甲产品	乙产品	合计
合格品
次品

（2）已知生产件甲产品，若为合格品，则可盈利元，若为次品，则亏损元；生产件乙产品，若为合格品，则可盈利元，若为次品，则亏损元.记为生产件甲产品和件乙产品所得的总利润，求随机变量的分布列和数学期望（将产品的合格率作为抽检一件这种产品为合格品的概率）

参考公式：

【题目】在如图所示的几何体中，面CDEF为正方形，平面ABCD为等腰梯形，AB//CD，AB =2BC，点Q为AE的中点.

（1）求证：AC//平面DQF；

（2）若∠ABC=60°，AC⊥FB，求BC与平面DQF所成角的正弦值.

【题目】某校名学生参加军事冬令营活动，活动期间各自扮演一名角色进行分组游戏，角色按级别从小到大共种，分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式，可以人一组或者人一组.如果人一组，则必须角色相同；如果人一组，则人角色相同或者人为级别连续的个不同角色.已知这名学生扮演的角色有名士兵和名司令，其余角色各人，现在新加入名学生，将这名学生分成组进行游戏，则新加入的学生可以扮演的角色的种数为________.