题目内容
【题目】已知函数![]() .
.
(1)求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求正整数
恒成立,求正整数![]() 的最小值.
的最小值.
【答案】(1)![]() ;
;
(2)1
【解析】
(1)求出切线斜率![]() ,切点坐标
,切点坐标![]() ,即可求得切线方程;
,即可求得切线方程;
(2)分离参数得![]() 对
对![]() 恒成立,构造新的函数
恒成立,构造新的函数![]() ,对
,对![]() 求导,得
求导,得![]() ,再构造函数
,再构造函数![]() .再求
.再求![]() ,分析
,分析![]() 的单调性,利用零点存在定理发现
的单调性,利用零点存在定理发现![]() 在区间
在区间![]() 上存在一个零点
上存在一个零点![]() ,由
,由![]() 得
得![]() .同时可得
.同时可得![]() 时,
时,![]() 单调递增,
单调递增,![]() 时,
时,![]() 单调递减,则
单调递减,则![]() ,则
,则![]() .又因为
.又因为![]() ,m为正整数,所以
,m为正整数,所以![]() 的最小值是1.
的最小值是1.
解:(1)![]() ,
,
![]() 切线的斜率为
切线的斜率为![]() ,
,
又![]() ,
,
![]() 所求切线的方程为
所求切线的方程为![]() ;
;
(2)当![]() 时,
时,![]() 整理可得
整理可得![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
![]() ,
,![]() ,
,
![]() 在区间
在区间![]() 上存在一个零点
上存在一个零点![]() ,
,
此时![]() ,即
,即![]() ,
,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ,函数
,函数![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,即
,即![]() ,函数
,函数![]() 单调递减,
单调递减,
![]() 有极大值,即最大值为
有极大值,即最大值为
![]() ,
,
则![]() ,
,
![]() ,
,
![]() 正整数
正整数![]() 的最小值是1.
的最小值是1.

练习册系列答案
相关题目
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸.呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院![]() 人进行了问卷调查得到了如下的列联表:
人进行了问卷调查得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 |
| ||
女 |
| ||
合计 |
|
已知在全部![]() 人中随机抽取
人中随机抽取![]() 人,抽到患心肺疾病的人的概率为
人,抽到患心肺疾病的人的概率为![]() .
.
(1)请将上面的列联表补充完整,并判断是否有![]() 的把握认为患心肺疾病与性别有关?请说明你的理由;
的把握认为患心肺疾病与性别有关?请说明你的理由;
(2)已知在不患心肺疾病的![]() 位男性中,有
位男性中,有![]() 位从事的是户外作业的工作.为了指导市民尽可能地减少因雾霾天气对身体的伤害,现从不患心肺疾病的
位从事的是户外作业的工作.为了指导市民尽可能地减少因雾霾天气对身体的伤害,现从不患心肺疾病的![]() 位男性中,选出
位男性中,选出![]() 人进行问卷调查,求所选的
人进行问卷调查,求所选的![]() 人中至少有一位从事的是户外作业的概率.
人中至少有一位从事的是户外作业的概率.
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式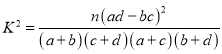 ,其中
,其中![]() )
)