题目内容
17．计算$\frac{i-2\sqrt{3}}{1+2\sqrt{3}i}$+（5+i19）-（$\frac{1+i}{\sqrt{2}}$）22．分析 直接利用复数代数形式的乘除运算及虚数单位i的运算性质得答案．
解答 解：$\frac{i-2\sqrt{3}}{1+2\sqrt{3}i}$+（5+i19）-（$\frac{1+i}{\sqrt{2}}$）22
=$\frac{（-2\sqrt{3}+i）（1-2\sqrt{3}i）}{（1+2\sqrt{3}i）（1-2\sqrt{3}i）}+（5-i）-$$（\frac{2i}{2}）^{11}$
=$\frac{13i}{13}+5-i+i$
=5+i．
点评 本题考查复数代数形式的乘除运算，考查了虚数单位i的运算性质，是基础的计算题．
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
8．
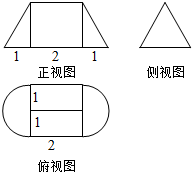一个几何体的侧视图是边长为2的正三角形，正视图与俯视图的尺寸如图所示，则此几何体的表面积为（ ）
一个几何体的侧视图是边长为2的正三角形，正视图与俯视图的尺寸如图所示，则此几何体的表面积为（ ）| A． | 12+2$\sqrt{3}$+3π | B． | 12+3π | C． | 2$\sqrt{3}$+$\frac{{\sqrt{3}π}}{3}$ | D． | 2$\sqrt{3}$+$\sqrt{3}$π |
12．若a＞1，b＞1，log2a•log2b=16，则log2（ab）的最小值为（ ）
| A． | -4 | B． | 8 | C． | -8 | D． | 4 |