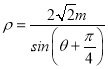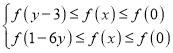题目内容
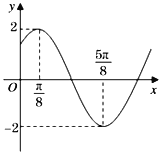
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,又函数![]() .
.
(1)求函数![]() 的单调减区间;
的单调减区间;
(2)设△ABC的内角A,B,C的对边分别为a,b,c,又![]() ,且锐角C满足
,且锐角C满足![]() ,若sinB=2sinA,求a+b的值.
,若sinB=2sinA,求a+b的值.
【答案】(1)![]() ;(2)3
;(2)3
【解析】
(1)由函数f(x)的部分图象可得A,可求函数的周期,利用正弦函数的周期公式可求ω的值,又函数图象过点![]() ,结合范围0<φ<π,可求
,结合范围0<φ<π,可求![]() ,可得f(x),g(x)的解析式,进而利用余弦函数的图象和性质可求其单调减区间.
,可得f(x),g(x)的解析式,进而利用余弦函数的图象和性质可求其单调减区间.
(2)由![]() ,得cos2C
,得cos2C![]() ,结合范围0
,结合范围0![]() ,可求C的值,由正弦定理得
,可求C的值,由正弦定理得![]() ,由余弦定理得3=a2+b2﹣ab,即可解得a,b的值,从而得解.
,由余弦定理得3=a2+b2﹣ab,即可解得a,b的值,从而得解.
解:(1)由函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象可得A=2,
由于![]() ,即T=π,
,即T=π,
则![]() ,
,
又函数图象过点![]() ,
,
则![]() ,
,
即![]() ,
,
又0<φ<π,
即![]() ,
,
即![]() ,
,
则![]() ,
,
由2kπ≤2x≤2kπ+π,k∈Z,得kπ≤x≤kπ![]() ,k∈Z,
,k∈Z,
所以函数g(x)的单调减区间为[kπ,kπ![]() ],k∈Z.
],k∈Z.
(2)由![]() ,得cos2C
,得cos2C![]() ,
,
因为0![]() ,
,
所以0<2C<π,
所以2C![]() ,可得
,可得![]() ,
,
又sinB=2sinA,由正弦定理得![]() ,①
,①
由余弦定理,得![]() ,可得:
,可得:![]() ,②.
,②.
由①②:![]() ,解得a=1,b=2,
,解得a=1,b=2,
所以a+b=3.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目