题目内容
【题目】已知定义在R上的奇函数f（x）＝ex﹣ae﹣x+2sinx满足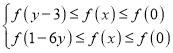
，则z＝x﹣lny的最小值是（ ）
A.﹣ln6B.﹣2C.ln6D.2
【答案】B
【解析】
由已知可求a，然后对函数求导，结合导数可判断函数的单调性，进而可得关于x，y的不等式组，结合线性规划知识即可求解
解：由题意f（0）＝1﹣a＝0可得a＝1，
所以f（x）＝ex﹣e﹣x+2sinx，
2+2cosx≥0，
故f（x）在R上单调递增，则
，
作出可行域如图所示，其中A（0，
），B（0，3），C（
，
），
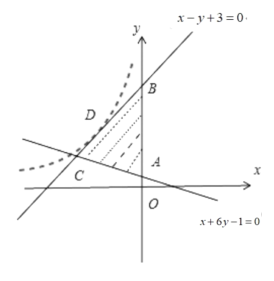
设y＝ex﹣z，则由图象可知，设y＝x+3与y＝ex﹣z相切于点D（x0，y0），
由y′＝ex﹣z，令
1可得x0＝z，
，
故y＝x+3与y＝ex﹣z相切于点D（﹣2，1）时，z取得最小值zmin＝﹣2.
故选：B
练习册系列答案
相关题目
