Question

【题目】在直角坐标系xOy中，曲线C的参数方程为（θ为参数），在以O为极点，x轴的正半轴为极轴的极坐标系中，直线l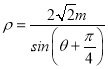：（m为常数）.

（1）求曲线C的普通方程与直线l的直角坐标方程；

（2）若直线l与曲线C相交于A、B两点，当|AB|=4时，求实数m的值.

Answer 1

【答案】（1）（x﹣1）2+（y+1）2=16，x+y﹣4m=0；（2）±.

【解析】

（1）由参数方程、极坐标方程与直角坐标方程的互化求解即可；

（2）由直线与圆的位置关系，结合点到直线的距离公式求解即可.

解:（1）曲线C的参数方程为（θ为参数），

由,消参数θ可得:

曲线C的普通方程为（x﹣1）2+（y+1）2=16，

直线l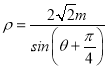：，即ρsinθ+ρcosθ=4m，

结合可得:

直线l的直角坐标方程为x+y﹣4m=0；

（2）由题意，圆心到直线的距离d2，

∴2，

∴m=±.