题目内容
【题目】如图,矩形ABCD中,![]() ,
,![]() ,E,F分别为AD,AB中点,M为线段BC上的一个动点,现将
,E,F分别为AD,AB中点,M为线段BC上的一个动点,现将![]() ,
,![]() ,分别沿EC,EF折起,使A,D重合于点P.设PM与平面BCEF所成角为
,分别沿EC,EF折起,使A,D重合于点P.设PM与平面BCEF所成角为![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,则( )
,则( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
过![]() 作
作![]()
![]() 平面
平面![]() ,作出三个二面角
,作出三个二面角![]() ,二面角
,二面角![]() 的平面角,二面角
的平面角,二面角![]() 的平面角,通过原平面图形计算可得这三个角的大小关系.从而得出结论.
的平面角,通过原平面图形计算可得这三个角的大小关系.从而得出结论.
在![]() 翻折过程中,A点在底面的投影在过点A且垂直EF的直线上(设垂足为I),同理在
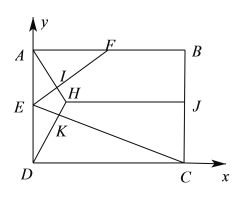
翻折过程中,A点在底面的投影在过点A且垂直EF的直线上(设垂足为I),同理在![]() 翻折过程中,D点在底面的投影在过点D且垂直EC的直线上(设垂足为K),设点P在底面的投影为点H,过点H向BC作垂线HJ(垂足为J),
翻折过程中,D点在底面的投影在过点D且垂直EC的直线上(设垂足为K),设点P在底面的投影为点H,过点H向BC作垂线HJ(垂足为J),
把![]() ,
,![]() 摊平到原来的平面图形,如下右图,
摊平到原来的平面图形,如下右图,![]() 就是
就是![]() 和
和![]() 延长线的交点,由已知可得
延长线的交点,由已知可得![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,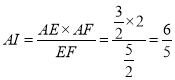 ,同理可得
,同理可得![]() ,
,![]() ,则在左图中知易得
,则在左图中知易得![]() ,由二面角的定义知
,由二面角的定义知![]() ,所以
,所以![]() ,
,
又在右图中,以![]() ,
,![]() 为
为![]() 轴建立平面直角坐标系,
轴建立平面直角坐标系,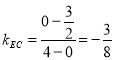 ,则
,则![]() ,直线
,直线![]() 方程为
方程为![]() ,同理直线
,同理直线![]() 的方程为
的方程为![]() ,由
,由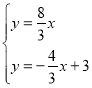 得
得![]() ,即
,即![]() ,∴
,∴![]() ,∴
,∴![]() ,所以二面角
,所以二面角![]() 的平面角小于二面角
的平面角小于二面角![]() 的平面角,显然
的平面角,显然![]() 不大于二面角
不大于二面角![]() 的平面角,∴
的平面角,∴![]() ,综上可知
,综上可知![]() ,
,
故选:D


练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目