题目内容
数列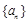 的首项
的首项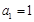 ,前
,前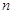 项和为
项和为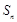 ,满足关系
,满足关系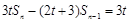 (
(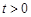 ,
,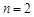 ,3,4…)
,3,4…)
(1)求证:数列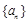 为等比数列;
为等比数列;
(2)设数列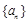 的公比为
的公比为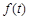 ,作数列
,作数列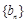 ,使
,使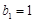 ,
,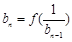 .(
.(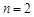 ,3,4…)求
,3,4…)求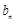
(3)求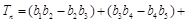 …
…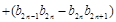 的值
的值
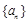 的首项
的首项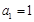 ,前
,前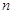 项和为
项和为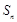 ,满足关系
,满足关系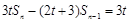 (
(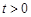 ,
,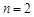 ,3,4…)
,3,4…)(1)求证:数列
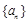 为等比数列;
为等比数列;(2)设数列
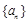 的公比为
的公比为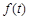 ,作数列
,作数列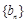 ,使
,使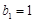 ,
,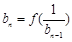 .(
.(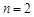 ,3,4…)求
,3,4…)求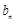
(3)求
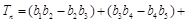 …
…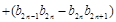 的值
的值(1)见解析(2)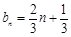 (3)
(3)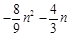
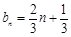 (3)
(3)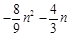
(1)由已知3tSn-(2t+3)Sn-1=3t,可得3tsn-1-(2t+3)sn-2=3t,两式相减可得数列an与an-1的递推关系,从而可证.
(2)把f(t)的解析式代入bn,进而可知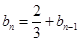 ,判断出{bn}是一个首项为1,公差为
,判断出{bn}是一个首项为1,公差为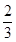 的等差数列.进而根据等差数列的通项公式求得答案.
的等差数列.进而根据等差数列的通项公式求得答案.
(3){bn}是等差数列,用分组法求得数列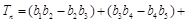 …
…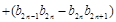 的和.
的和.
解:(1)证:
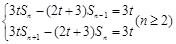 ,两式相减得
,两式相减得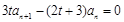 ,
,
又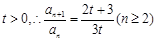 ,又当
,又当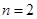 时,
时,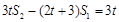 ,
,
即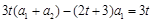 ,得
,得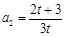 ,即
,即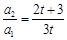 ,
,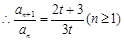
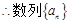 为等比数列
为等比数列
(2)由已知得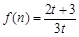 ,
,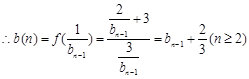
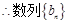 是以
是以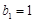 为首项,
为首项,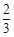 为公比的等比数列.
为公比的等比数列.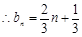
(3)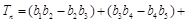 …
…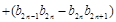
=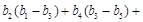 ……
……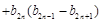
=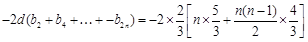 =
=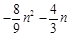
(2)把f(t)的解析式代入bn,进而可知
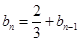 ,判断出{bn}是一个首项为1,公差为
,判断出{bn}是一个首项为1,公差为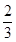 的等差数列.进而根据等差数列的通项公式求得答案.
的等差数列.进而根据等差数列的通项公式求得答案.(3){bn}是等差数列,用分组法求得数列
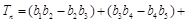 …
…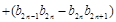 的和.
的和.解:(1)证:
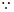
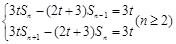 ,两式相减得
,两式相减得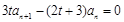 ,
,又
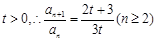 ,又当
,又当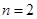 时,
时,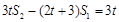 ,
,即
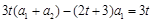 ,得
,得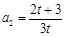 ,即
,即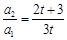 ,
,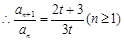
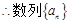 为等比数列
为等比数列(2)由已知得
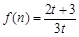 ,
,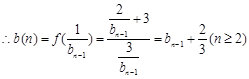
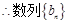 是以
是以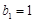 为首项,
为首项,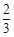 为公比的等比数列.
为公比的等比数列.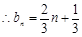
(3)
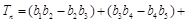 …
…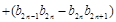
=
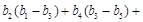 ……
……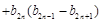
=
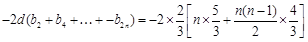 =
=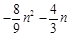

练习册系列答案
相关题目
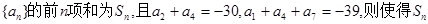 达到最小值的n是( )
达到最小值的n是( )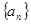 满足
满足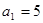 ,
,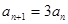 ,写出这个数列的前5项并归纳猜想通项公式。
,写出这个数列的前5项并归纳猜想通项公式。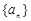 中,
中,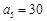 ,
,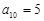 ,则
,则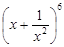 的展开式中的常数项是该数
的展开式中的常数项是该数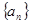 为等差数列,公差
为等差数列,公差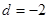 ,
,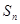 为其前
为其前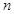 项和,若
项和,若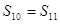 ,则
,则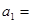 ( )
( )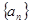 中,
中,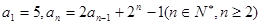 ,若存在实数
,若存在实数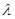 ,使得数列
,使得数列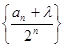 为等差数列,则
为等差数列,则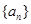 中,
中,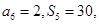 则
则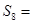 ( )
( )