题目内容
在等差数列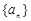 中,
中,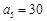 ,
,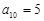 ,则
,则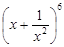 的展开式中的常数项是该数
的展开式中的常数项是该数
列的
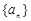 中,
中,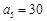 ,
,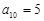 ,则
,则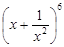 的展开式中的常数项是该数
的展开式中的常数项是该数列的
| A.第9项 | B.第8项 | C.第7项 | D.第6项 |
B
由已知条件得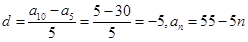 .
.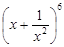 的展开式的通项是
的展开式的通项是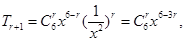 常数项是
常数项是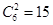 .为等差数列
.为等差数列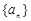 中的第8项.
中的第8项.
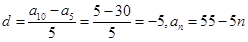 .
.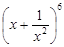 的展开式的通项是
的展开式的通项是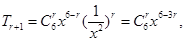 常数项是
常数项是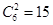 .为等差数列
.为等差数列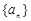 中的第8项.
中的第8项.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
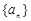 中,
中,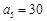 ,
,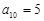 ,则
,则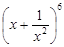 的展开式中的常数项是该数
的展开式中的常数项是该数| A.第9项 | B.第8项 | C.第7项 | D.第6项 |
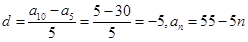 .
.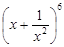 的展开式的通项是
的展开式的通项是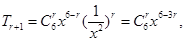 常数项是
常数项是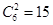 .为等差数列
.为等差数列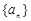 中的第8项.
中的第8项.
 阅读快车系列答案
阅读快车系列答案