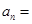题目内容
(12分)设集合W是满足下列两个条件的无穷数列{an}的集合:
①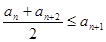 ②
②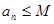 ,其中n∈N*,M是与n无关的常数
,其中n∈N*,M是与n无关的常数
(1)若{an}是等差数列,Sn是其前n项的和,a3=4,S3=18,试探究{Sn}与集合W之间的关系;
(2)设数列{bn}的通项为bn=5n-2n,且{bn}∈W,M的最小值为m,求m的值;
(3)在(2)的条件下,设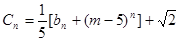 ,求证:数列{Cn}中任意不同的三项都不能成为等比数列.
,求证:数列{Cn}中任意不同的三项都不能成为等比数列.
①
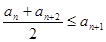 ②
②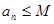 ,其中n∈N*,M是与n无关的常数
,其中n∈N*,M是与n无关的常数(1)若{an}是等差数列,Sn是其前n项的和,a3=4,S3=18,试探究{Sn}与集合W之间的关系;
(2)设数列{bn}的通项为bn=5n-2n,且{bn}∈W,M的最小值为m,求m的值;
(3)在(2)的条件下,设
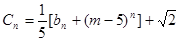 ,求证:数列{Cn}中任意不同的三项都不能成为等比数列.
,求证:数列{Cn}中任意不同的三项都不能成为等比数列. (1) {Sn}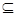 W ; (2) M的最小值为7; (3) 见解析.
W ; (2) M的最小值为7; (3) 见解析.
 W ; (2) M的最小值为7; (3) 见解析.
W ; (2) M的最小值为7; (3) 见解析.第一问利用Sn=-n2+9n
 满足①
满足①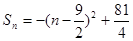 当n=4或5时,Sn取最大值20
当n=4或5时,Sn取最大值20
第二问中bn+1-bn=5-2n可知{bn}中最大项是b3=7
∴ M≥7 M的最小值为7 …………8分
第三问中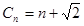 ,假设{Cn}中存在三项bp、bq、br(p、q、r互不相等)
,假设{Cn}中存在三项bp、bq、br(p、q、r互不相等)
成等比数列,则bq2=bp·br
∴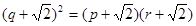
∴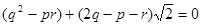
∵ p、q、r∈N*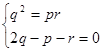
∴ p=r与p≠r矛盾
解:(1) Sn=-n2+9n
 满足①
满足①
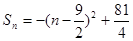 当n=4或5时,Sn取最大值20
当n=4或5时,Sn取最大值20
∴Sn≤20满足② ∴{Sn}∈W …………4分
(2) bn+1-bn=5-2n可知{bn}中最大项是b3=7
∴ M≥7 M的最小值为7 …………8分
(3)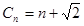 ,假设{Cn}中存在三项bp、bq、br(p、q、r互不相等)
,假设{Cn}中存在三项bp、bq、br(p、q、r互不相等)
成等比数列,则bq2=bp·br
∴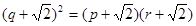
∴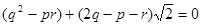
∵ p、q、r∈N*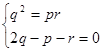
∴ p=r与p≠r矛盾
∴ {Cn}中任意不同的三项都不能成为等比数列 …………12分
 满足①
满足①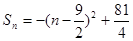 当n=4或5时,Sn取最大值20
当n=4或5时,Sn取最大值20第二问中bn+1-bn=5-2n可知{bn}中最大项是b3=7
∴ M≥7 M的最小值为7 …………8分
第三问中
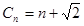 ,假设{Cn}中存在三项bp、bq、br(p、q、r互不相等)
,假设{Cn}中存在三项bp、bq、br(p、q、r互不相等)成等比数列,则bq2=bp·br
∴
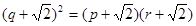
∴
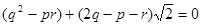
∵ p、q、r∈N*
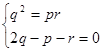
∴ p=r与p≠r矛盾
解:(1) Sn=-n2+9n
 满足①
满足①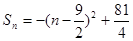 当n=4或5时,Sn取最大值20
当n=4或5时,Sn取最大值20∴Sn≤20满足② ∴{Sn}∈W …………4分
(2) bn+1-bn=5-2n可知{bn}中最大项是b3=7
∴ M≥7 M的最小值为7 …………8分
(3)
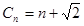 ,假设{Cn}中存在三项bp、bq、br(p、q、r互不相等)
,假设{Cn}中存在三项bp、bq、br(p、q、r互不相等)成等比数列,则bq2=bp·br
∴
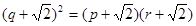
∴
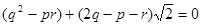
∵ p、q、r∈N*
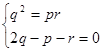
∴ p=r与p≠r矛盾
∴ {Cn}中任意不同的三项都不能成为等比数列 …………12分

练习册系列答案
相关题目
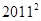 .
.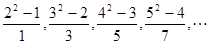 ,则此数列的通项公式
,则此数列的通项公式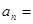 _____;
_____;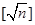 表示不超过
表示不超过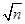 的最大整数。
的最大整数。
 。
。 根据以上规
根据以上规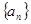 中,
中,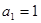 ,
,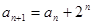 ,则
,则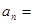 .
.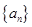 中,
中,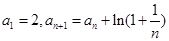 ,则
,则