题目内容
【题目】如果一个函数
的图像是一个中心对称图形，关于点
对称，那么将的图像向左平移m个单位再向下平移n的单位后得到一个关于原点对称的函数图像.即函数
为奇函数.那么下列命题中真命题的个数是（ ）
①二次函数
（
）的图像肯定不是一个中心对称图形；
②三次函数
（）的图像肯定是一个中心对称图形；
③函数
（
且
）的图像肯定是一个中心对称图形.
A.0个B.1个C.2个D.3个
【答案】D
【解析】
①根据二次函数的图象特征直接判断结果；
②三次函数
（
）向左平移
个单位，再向下平移
个单位后得到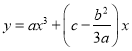
，是奇函数，所以根据定义也可判断三次函数是中心对称；
③
，根据对称公式直接判断对称中心.
①二次函数
（）一定是轴对称图形，不可能是中心对称图形,故正确；
②三次函数（）向左平移个单位，再向下平移个单位后得到
当
时，
，
此时函数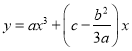，平移后的函数是奇函数，关于原点对称，
则函数（）也一定是中心对称图形，故正确；
③
（
且
），
，
，
关于点
对称，故正确.
故选：D
名校课堂系列答案
【题目】某大学为了更好提升学校文化品位，发挥校园文化的教育功能特举办了校园文化建设方案征集大赛，经评委会初评，有两个优秀方案入选.为了更好充分体现师生的主人翁意识，组委会邀请了100名师生代表对这两个方案进行登记评价（登记从高到低依次为
），评价结果对应的人数统计如下表：
编号 | 等级 | ||||
|
|
|
|
| |
1号方案 | 8 | 41 | 26 | 15 | 10 |
2号方案 | 7 | 33 | 20 | 20 | 20 |
（Ⅰ）若从对1号方案评价为
的师生中任选3人，求这3人中至少有1人对1号方案评价为
的概率；
（Ⅱ）在
级以上（含级），可获得2万元的奖励，级奖励
万元，
级无奖励.若以此表格数据估计概率，随机请1名师生分别对两个方案进行独立评价，求两个方案获得的奖励总金额
（单位：万元）的分布列和数学期望．
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题．该企业为了检查生产该产品的甲、乙两条流水线的生产情况，随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本，测出它们的这一项质量指标值．若该项质量指标值落在
内，则为合格品，否则为不合格品．如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图．
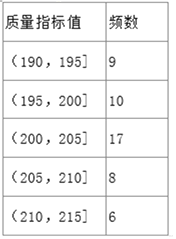
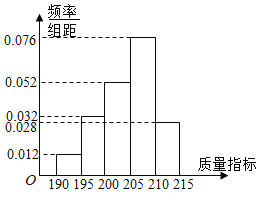
（1）根据频率分布直方图，估计乙流水线生产的产品该质量指标值的中位数；
（2）若将频率视为概率，某个月内甲、乙两条流水线均生产了5000件产品，则甲、乙两条流水线分别生产出不合格品约多少件？
（3）根据已知条件完成下面
列联表，并回答是否有
的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”？
甲流水线 | 乙流水线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附：
，其中
.
临界值表：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计，绘制了频率分布直方图（如图所示），规定80分及以上者晋级成功，否则晋级失败．
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
（1）求图中
的值；
（2）根据已知条件完成下面
列联表，并判断能否有
的把握认为“晋级成功”与性别有关？
（3）将频率视为概率，从本次考试的所有人员中，随机抽取4人进行约谈，记这4人中晋级失败的人数为
，求的分布列与数学期望
．
（参考公式：
，其中
）
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
