题目内容
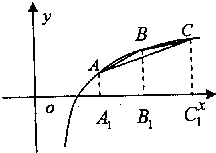
在函数f(x)=lgx的图象上有三点A、B、C,横坐标依次是m-1,m,m+1(m>2).
(1)试比较f(m-1)+f(m+1)与2f(m)的大小;
(2)求△ABC的面积S=g(m)的值域.
(1)试比较f(m-1)+f(m+1)与2f(m)的大小;
(2)求△ABC的面积S=g(m)的值域.

(1)∵f(m-1)+f(m+1)=lg(m-1)+lg(m+1)=lg(m2-1),
2f(m)=2lgm=lgm2>lg(m2-1),
∴f(m-1)+f(m+1)<2f(m).
(2)△ABC的面积S=g(m)=SABB1A1+SCBB1C1-SCBA1C1
=
[lg(m-1)+lgm]+
[lg(m+1)+lgm]-
[lg(m-1)+lg(m+1)]×2
=
lg[
]=
lg(1+
),
∵m>2时,S=g(m)单调递减,
∴0<S<
lg
,
故△ABC的面积S的值域为 (0,
lg
).

2f(m)=2lgm=lgm2>lg(m2-1),
∴f(m-1)+f(m+1)<2f(m).
(2)△ABC的面积S=g(m)=SABB1A1+SCBB1C1-SCBA1C1
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| m2 |
| (m+1)(m-1) |
| 1 |
| 2 |
| 1 |
| m2-1 |
∵m>2时,S=g(m)单调递减,
∴0<S<
| 1 |
| 2 |
| 4 |
| 3 |
故△ABC的面积S的值域为 (0,
| 1 |
| 2 |
| 4 |
| 3 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
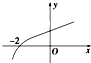
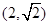 ,则 f(4)= .
,则 f(4)= .