题目内容
已知函数y=loga(3-ax),(a>0,a≠1)在[0,1]上单调递减,则实数a的取值范围为______.
设t=g(x)=3-ax,则∵a>0,a≠1,∴t=3-ax在定义域上单调递减,
要使函数y=loga(3-ax),(a>0,a≠1)在[0,1]上单调递减,
则有y=logat在定义域上为单调递增,
则须有
,即
,解得1<a<3.
故实数a的取值范围为1<a<3.
故答案为:(1,3).
要使函数y=loga(3-ax),(a>0,a≠1)在[0,1]上单调递减,
则有y=logat在定义域上为单调递增,
则须有
|
|
故实数a的取值范围为1<a<3.
故答案为:(1,3).

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
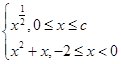 ,其中c>0.那么f(x)的零点是________;若f(x)的值域是
,其中c>0.那么f(x)的零点是________;若f(x)的值域是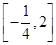 ,则c的取值范围是________.
,则c的取值范围是________.