题目内容
正项数列{an}满足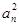 -(2n-1)an-2n=0.
-(2n-1)an-2n=0.
(1)求数列{an}的通项公式an;
(2)令bn=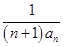 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
(1) an=2n (2) Tn=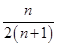
解析解:(1)已知an与n的关系式,求an,这一类题目应把式子进行变形,得an=f(n),从而求出通项公式.
由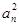 -(2n-1)an-2n=0,
-(2n-1)an-2n=0,
得(an-2n)(an+1)=0.
故an=-1(因数列为正项数列,舍去)或an=2n.
(2)因bn=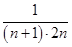 =
= (
(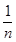 -
-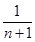 ),
),
所以Tn=b1+b2+b3+…+bn
= (
(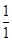 -
- )+
)+ (
( -
-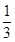 )+
)+ (
(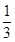 -
- )+…+
)+…+ (
(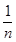 -
-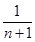 )
)
= (
(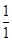 -
- +
+ -
-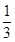 +
+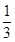 -
- +…+
+…+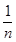 -
-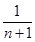 )
)
= (1-
(1-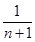 )
)
=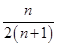 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
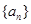 中,已知
中,已知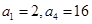 .
.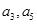 分别为等差数列
分别为等差数列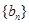 的第3项和第5项,试求数列
的第3项和第5项,试求数列 项和
项和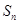 .
.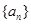 ,其前
,其前 项和
项和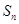 满足
满足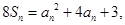 且
且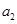 是
是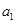 和
和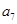 的等比中项..
的等比中项..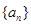 的通项公式;
的通项公式;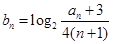 ,求数列
,求数列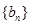 的前99项和.
的前99项和.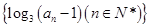 为等差数列,且
为等差数列,且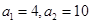 .
.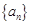 的通项公式;
的通项公式;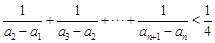 .
.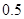 万人,从2023年开始到2032年每年人口为上一年的99%.
万人,从2023年开始到2032年每年人口为上一年的99%. 年的人口总数
年的人口总数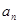 的表达式(注:2013年为第一年);
的表达式(注:2013年为第一年);