题目内容
已知等差数列{an}的首项为a,公差为d,且方程ax2-3x+2=0的解为1,d.
(1)求{an}的通项公式及前n项和公式;
(2)求数列{3n-1an}的前n项和Tn.
(1) an=2n-1 Sn=n2 (2) Tn=1+(n-1)·3n
解析解:(1)方程ax2-3x+2=0的两根为1,d.
所以a=1,d=2.
由此知an=1+2(n-1)=2n-1,前n项和Sn=n2.
(2)令bn=3n-1an=(2n-1)·3n-1,
则Tn=b1+b2+b3+…+bn=1·1+3·3+5·32+…+(2n-1)·3n-1,
3Tn=1·3+3·32+5·32+…+(2n-3)·3n-1+(2n-1)·3n,
两式相减,得-2Tn=1+2·3+2·32+…+2·3n-1-(2n-1)·3n=1+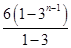 -(2n-1)·3n=-2-2(n-1)·3n.
-(2n-1)·3n=-2-2(n-1)·3n.
∴Tn=1+(n-1)·3n.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
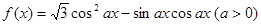 的图像与直线
的图像与直线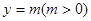 相切,并且切点横坐标依次成公差为
相切,并且切点横坐标依次成公差为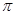 的等差数列.
的等差数列.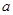 和
和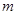 的值;
的值;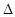 ABC中a、b、c分别是∠A、∠B、∠C的对边.若
ABC中a、b、c分别是∠A、∠B、∠C的对边.若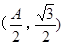 是函数
是函数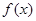 图象的一个对称中心,且a=4,求
图象的一个对称中心,且a=4,求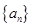 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项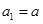 ,
,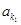 、
、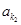 、
、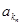 恰为等比数列,且
恰为等比数列,且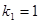 ,
,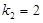 ,
,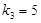 .
.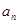 (用
(用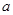 表示);
表示);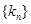 的前
的前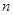 项和为
项和为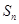 ,求
,求 ,证明数列{bn}是等差数列,并求其前n项和Tn.
,证明数列{bn}是等差数列,并求其前n项和Tn.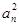 -(2n-1)an-2n=0.
-(2n-1)an-2n=0.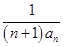 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.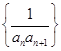 的前n项和,若Tn≤
的前n项和,若Tn≤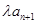 ¨对
¨对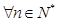 恒成立,求实数
恒成立,求实数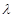 的最小值.
的最小值. }的前n项和Sn.
}的前n项和Sn.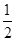 an,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的最小的正整数n.
an,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的最小的正整数n.