题目内容
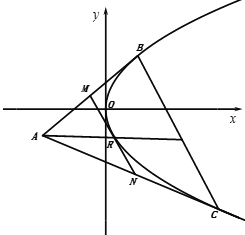
【题目】在平面直角坐标系![]() 中,
中,![]() 为坐标原点,C、D两点的坐标为
为坐标原点,C、D两点的坐标为![]() ,曲线
,曲线![]() 上的动点P满足
上的动点P满足![]() .又曲线
.又曲线![]() 上的点A、B满足
上的点A、B满足![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若点A在第一象限,且![]() ,求点A的坐标;
,求点A的坐标;
(3)求证:原点到直线AB的距离为定值.
【答案】(1)![]() (2)
(2)![]() (3)证明见解析
(3)证明见解析
【解析】
(1)由![]() ,
,![]() 知,曲线
知,曲线![]() 是以
是以![]() 、
、![]() 为焦点,长轴
为焦点,长轴![]() 的椭圆,即可求曲线
的椭圆,即可求曲线![]() 的方程(2)设直线
的方程(2)设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,与椭圆方程联立,由
,与椭圆方程联立,由![]() 知
知![]() ,即可求点
,即可求点![]() 的坐标(3)分类讨论,设直线
的坐标(3)分类讨论,设直线![]() 的方程
的方程![]() ,与椭圆方程联立,求出原点到直线
,与椭圆方程联立,求出原点到直线![]() 的距离,即可证明原点到直线
的距离,即可证明原点到直线![]() 的距离为定值.
的距离为定值.
(1)由![]() ,
,![]() 知,曲线E是以C、D为焦点,长轴
知,曲线E是以C、D为焦点,长轴![]() 的椭圆,
的椭圆,
设其方程为![]() ,则有
,则有![]() ,
,
∴曲线E的方程为![]()
(2)设直线OA的方程为![]() ,则直线OB的方程为
,则直线OB的方程为![]()
由则 得
得![]() ,解得
,解得![]()
同理,由则 解得
解得![]() .
.
由![]() 知
知![]() ,
,
即![]()
解得![]() ,因点A在第一象限,故
,因点A在第一象限,故![]() ,
,
此时点A的坐标为![]()
(3)设![]() ,
,![]() ,
,
当直线AB平行于坐标轴时,由![]() 知A、B两点之一为
知A、B两点之一为![]() 与椭圆的交点,
与椭圆的交点,
由
解得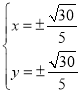 ,
,
此时原点到直线AB的距离为![]() ,
,
当直线AB不平行于坐标轴时,设直线AB的方程![]() ,
,
由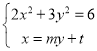 得
得![]()
由![]() 得
得![]()
即![]()
因![]()
代入得![]() 即
即![]()
原点到直线AB的距离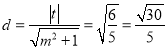 .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目