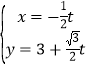题目内容
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),曲线C2的参数方程为
为参数),曲线C2的参数方程为![]() (
(![]() 为参数).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α 与C1,C2 各有一个交点.当 α=0时,这两个交点间的距离为2,当 α=
为参数).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α 与C1,C2 各有一个交点.当 α=0时,这两个交点间的距离为2,当 α=![]() 时,这两个交点重合.
时,这两个交点重合.
(1) 求曲线C1,C2的直角坐标方程
(2) 设当 α=![]() 时,l与C1,C2的交点分别为A1,B1,当 α=-
时,l与C1,C2的交点分别为A1,B1,当 α=-![]() 时,l与C1,C2的交点分别为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点分别为A2,B2,求四边形A1A2B2B1的面积.
【答案】(1)C1,C2的普通方程分别为x2+y2=1和![]() +y2=1,(2)
+y2=1,(2)![]()
【解析】
(1)令α=0和α=![]() 得a,b 值由参数方程与普通方程的互化求解得C1,C2的普通方程;(2)令α=
得a,b 值由参数方程与普通方程的互化求解得C1,C2的普通方程;(2)令α=![]() ,得A1,B1的横坐标,利用对称性得A1,B1关于x轴对称,得四边形A1A2B2B1为等腰梯形,利用面积公式求解即可
,得A1,B1的横坐标,利用对称性得A1,B1关于x轴对称,得四边形A1A2B2B1为等腰梯形,利用面积公式求解即可
由题C1 的普通方程为x2+y2=1;C2的普通方程为![]()
当α=0时,射线l与C1,C2交点的直角坐标分别为(1,0),(a,0),因为这两点间的距离为2,所以a=3.
当α=![]() 时,射线l与C1,C2交点的直角坐标分别为(0,1),(0,b),因为这两点重合,所以b=1.
时,射线l与C1,C2交点的直角坐标分别为(0,1),(0,b),因为这两点重合,所以b=1.
故C1,C2的普通方程分别为x2+y2=1和![]() +y2=1,
+y2=1,
(2)当α=![]() 时,射线l与C1交点A1的横坐标为x=
时,射线l与C1交点A1的横坐标为x=![]() ,与C2交点B1的横坐标为x′=
,与C2交点B1的横坐标为x′=![]() .
.
当α=-![]() 时,射线l与C1,C2的两个交点A2,B2分别与A1,B1关于x轴对称,因此四边形A1A2B2B1为梯形.
时,射线l与C1,C2的两个交点A2,B2分别与A1,B1关于x轴对称,因此四边形A1A2B2B1为梯形.
故四边形A1A2B2B1的面积为![]() .
.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】近几年来,“精准扶贫”是政府的重点工作之一,某地政府对240户贫困家庭给予政府资金扶助,以发展个体经济,提高家庭的生活水平.几年后,一机构对这些贫困家庭进行回访调查,得到政府扶贫资金数、扶贫贫困家庭数![]() (户)与扶贫后脱贫家庭数
(户)与扶贫后脱贫家庭数![]() (户)的数据关系如下:
(户)的数据关系如下:
政府扶贫资金数(万元) | 3 | 5 | 7 | 9 |
政府扶贫贫困家庭数 | 20 | 40 | 80 | 100 |
扶贫后脱贫家庭数 | 10 | 30 | 70 | 90 |
(Ⅰ)求几年来该地依靠“精准扶贫”政策的脱贫率是多少;(答案精准到0.1%)
(Ⅱ)从政府扶贫资金数为3万元和7万元并且扶贫后脱贫的家庭中按分层抽样抽取8户,再从这8户中随机抽取两户家庭,求这两户家庭的政府扶贫资金总和为10万元的概率.
【题目】某超市随机选取![]() 位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
| 甲 | 乙 | 丙 | 丁 |
| √ | × | √ | √ |
| × | √ | × | √ |
| √ | √ | √ | × |
| √ | × | √ | × |
85 | √ | × | × | × |
| × | √ | × | × |
(Ⅰ)估计顾客同时购买乙和丙的概率;
(Ⅱ)估计顾客在甲、乙、丙、丁中同时购买![]() 中商品的概率;
中商品的概率;
(Ⅲ)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?