��Ŀ����
����Ŀ��2018�꣬�й�ijʡ��һ��������������֯Ϊ������30��-60���Χ�尮���߾�����һ�ν�������������ÿ�˺�һλ����ѡ�ֽ���һ��������Ӯ�˾Ϳ��Խ��������Ͳ��ܽ����������������200�˰����䣨��λ���꣩�ֳ����飺��һ��![]() ���ڶ���
���ڶ���![]() ��������
��������![]() ��������
��������![]() ��������
��������![]() ��������
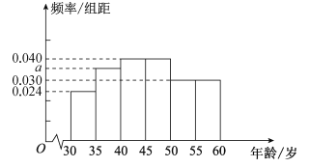
��������![]() ����ͼ�ǰ����������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ.
����ͼ�ǰ����������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ.
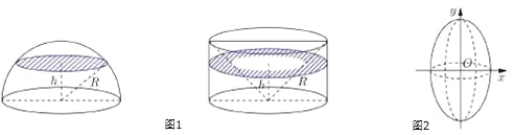
��1����ʵ��![]() ��ֵ��
��ֵ��
��2�������ڵ����顢�����顢�������а���ֲ��������ȡ10�ˣ�Ȼ��ӱ���ȡ����10���������ȡ3�˲μ���ʤ����.
�������������һ�˲μ���ʤ�����ĸ��ʣ�
����![]() Ϊ�μ���ʤ������3���е��������������
Ϊ�μ���ʤ������3���е��������������![]() �ķֲ��к���ѧ����
�ķֲ��к���ѧ����![]() .
.
���𰸡���1��![]() ��2����
��2����![]() �ڼ�����
�ڼ�����
��������
��1������Ƶ�ʺ�Ϊ![]() �з��̣��ⷽ�����
�з��̣��ⷽ�����![]() ��ֵ.��2�����÷ֲ������֪ʶ�����ÿ��ij�ȡ����. ���ùŵ���͵ĸ��ʼ��㹫ʽ��������������һ�˲μ���ʤ�����ĸ��ʣ������ó����ηֲ���֪ʶ������ֲ��к���ѧ����.
��ֵ.��2�����÷ֲ������֪ʶ�����ÿ��ij�ȡ����. ���ùŵ���͵ĸ��ʼ��㹫ʽ��������������һ�˲μ���ʤ�����ĸ��ʣ������ó����ηֲ���֪ʶ������ֲ��к���ѧ����.
�⣺��1��ֱ��ͼ�е����Ϊ5��
�ɵ�![]() ��
��
��![]() .
.
��2����ֱ��ͼ�пɵõ����������Ϊ![]() ���ˣ��������������Ϊ
���ˣ��������������Ϊ![]() ���ˣ��������������Ϊ
���ˣ��������������Ϊ![]() ���ˣ���
���ˣ���
���鹲100�ˣ������÷ֲ��������ȡ10�ˣ��������Ӧ��ȡ4�ˣ�������Ӧ��ȡ3�ˣ�������Ӧ��ȡ3��.
���������һ�˲μ���ʤ�����ĸ���![]() ��
��
��![]() �Ŀ���ȡֵΪ0��1��2��3��
�Ŀ���ȡֵΪ0��1��2��3��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() .
.

����Ŀ����������ָ��AQI��һ�ַ�ӳ�����ۿ��������ķ�����AQIָ�������������Ӧ�����ʾ��
AQI | 0��50 | 51��100 | 101��150 | 151��200 | 201��300 | 300���� |
�������� | �� | �� | �����Ⱦ | �ж���Ⱦ | �ض���Ⱦ | ������Ⱦ |
��ͼ��ij����2018��12��ȫ�µ�AQIָ���仯ͳ��ͼ��

����ͳ��ͼ�жϣ����н�����ȷ���ǣ�������
A. �����Ͽ�������µĿ�������Խ��Խ��
B. �����Ͽ���ǰ���µĿ����������ں����µĿ�������
C. ��AQI���ݿ���ǰ���µķ�����ں���µķ���
D. ��AQI���ݿ���ǰ���µ�ƽ��ֵС�ں���µ�ƽ��ֵ