题目内容
【题目】已知数列{an}和{bn}满足a1a2a3…an= ![]() (n∈N*).若{an}为等比数列,且a1=2,b3=6+b2 .
(n∈N*).若{an}为等比数列,且a1=2,b3=6+b2 .
(1)求an和bn;
(2)设cn= ![]() (n∈N*).记数列{cn}的前n项和为Sn .
(n∈N*).记数列{cn}的前n项和为Sn .
(i)求Sn;
(ii)求正整数k,使得对任意n∈N*均有Sk≥Sn .
【答案】
(1)解:∵a1a2a3…an= ![]() (n∈N*) ①,
(n∈N*) ①,
当n≥2,n∈N*时, ![]() ②,
②,
由①②知: ![]() ,
,
令n=3,则有 ![]() .
.
∵b3=6+b2,
∴a3=8.
∵{an}为等比数列,且a1=2,
∴{an}的公比为q,则 ![]() =4,
=4,
由题意知an>0,∴q>0,∴q=2.
∴ ![]() (n∈N*).
(n∈N*).
又由a1a2a3…an= ![]() (n∈N*)得:
(n∈N*)得:
![]() ,
,
![]() ,
,
∴bn=n(n+1)(n∈N*).
(2)解:(i)∵cn= ![]() =
= ![]() =
= ![]() .
.
∴Sn=c1+c2+c3+…+cn
= ![]()
= ![]()
= ![]()
= ![]() ;
;
(ii)因为c1=0,c2>0,c3>0,c4>0;
当n≥5时,
![]() ,
,
而
![]() =
= ![]() >0,
>0,
得
![]() ,
,
所以,当n≥5时,cn<0,
综上,对任意n∈N*恒有S4≥Sn,故k=4
【解析】(1)先利用前n项积与前(n﹣1)项积的关系,得到等比数列{an}的第三项的值,结合首项的值,求出通项an , 然后现利用条件求出通项bn;(2)(i)利用数列特征进行分组求和,一组用等比数列求和公式,另一组用裂项法求和,得出本小题结论;(ii)本小题可以采用猜想的方法,得到结论,再加以证明.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系 才能正确解答此题.
才能正确解答此题.

【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位: ![]() ).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布
).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记![]() 表示一天内抽取的16个零件中其尺寸在
表示一天内抽取的16个零件中其尺寸在![]() 之外的零件数,求
之外的零件数,求![]() 及
及![]() 的数学期望;
的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得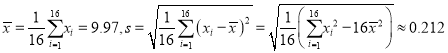 ,其中
,其中![]() 为
为
抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() (精确到0.01).
(精确到0.01).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
, ![]() .
.

