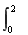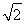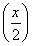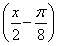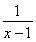Question

已知函数f(x)＝

(1)若x<a时，f(x)<1恒成立，求a的取值范围；

(2)若a≥－4时，函数f(x)在实数集R上有最小值，求实数a的取值范围．

 

Answer 1

（1）a≤log2 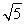（2）a>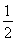时，函数f(x)有最小值

【解析】(1)因为x<a时，f(x)＝4x－4×2x－a，所以令t＝2x，则有0<t<2a.

当x<a时f(x)<1恒成立，转化为t2－4×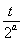<1，

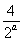即>t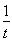－在t∈(0，2a)上恒成立．

令p(t)＝t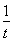－，t∈(0，2a)，则p′(t)＝1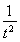＋>0，所以p(t)＝t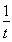－在(0，2a)上单调递增，

所以≥2a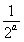－，所以2a≤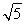，解得a≤log2 .

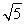(2)当x≥a时，f(x)＝x2－ax＋1，即f(x)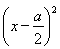＝＋1－，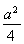

当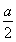≤a时，即a≥0时，f(x)min＝f(a)＝1；

当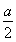>a时，即－4≤a<0，f(x)min＝f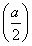＝1－.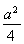

当x<a时，f(x)＝4x－4×2x－a，令t＝2x，t∈(0，2a)，则h(t)＝t2－t＝－，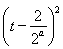

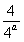当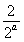<2a，即a> 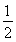时，h(t)min＝h＝－；

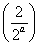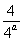当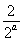≥2a，即a≤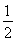时，h(t)在开区间t∈(0，2a)上单调递减，h(t)∈(4a－4，0)，无最小值．

综合x≥a与x<a，所以当a> 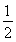时，1>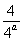－，函数f(x)min＝－；

当0≤a≤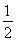时，4a－4<0<1，函数f(x)无最小值；

当－4≤a<0时，4a－4<－3≤1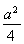－，函数f(x)无最小值．

综上所述，当a>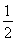时，函数f(x)有最小值．