题目内容
若向量a＝(cos θ，sin θ)，b＝(
，－1)，则|a－b|的最大值为( )
A．1 B．2 C．3 D．4
C
【解析】因为向量a＝(cos θ，sin θ)，b＝(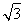
，－1)，所以|a|＝1，|b|＝2，a·b＝
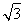cos θ－sin θ，所以|a－b|2＝a2＋b2－2a·b＝5－2(
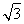cos θ－sin θ)＝5－4cos
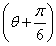，所以|a－b|2的最大值为9，因此|a－b|的最大值为3.
练习册系列答案
相关题目
题目内容
若向量a＝(cos θ，sin θ)，b＝(，－1)，则|a－b|的最大值为( )
A．1 B．2 C．3 D．4
C
【解析】因为向量a＝(cos θ，sin θ)，b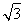＝(，－1)，所以|a|＝1，|b|＝2，a·b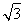＝cos θ－sin θ，所以|a－b|2＝a2＋b2－2a·b＝5－2(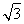cos θ－sin θ)＝5－4cos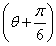，所以|a－b|2的最大值为9，因此|a－b|的最大值为3.
