题目内容
【题目】已知点![]() 、点
、点![]() 及抛物线
及抛物线![]() .
.
(1)若直线![]() 过点
过点![]() 及抛物线
及抛物线![]() 上一点
上一点![]() ,当
,当![]() 最大时求直线
最大时求直线![]() 的方程;
的方程;
(2)![]() 轴上是否存在点
轴上是否存在点![]() ,使得过点
,使得过点![]() 的任一条直线与抛物线
的任一条直线与抛物线![]() 交于点
交于点![]() ,且点
,且点![]() 到直线
到直线![]() 的距离相等?若存在,求出点
的距离相等?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据题意,设过点![]() 的直线方程为:
的直线方程为:![]() ,与
,与![]() .联立得:
.联立得:![]() , 然后再利用当直线与抛物线相切时,
, 然后再利用当直线与抛物线相切时,![]() 最大求解。
最大求解。
(2)先假设存在点![]() ,设过点
,设过点![]() 的直线方程为:
的直线方程为:![]() ,与
,与![]() .联立得:
.联立得:![]() ,根据点
,根据点![]() 到直线
到直线![]() 的距离相等,有
的距离相等,有![]() 关于x轴对称,即
关于x轴对称,即![]() 求解。
求解。
(1)根据题意,设过点![]() 的直线方程为:
的直线方程为:![]() ,
,
与![]() .联立得:
.联立得:![]() ,
,
直线![]() 过点
过点![]() 及抛物线
及抛物线![]() 上一点
上一点![]() ,
,
当![]() 最大时,则直线与抛物线相切,
最大时,则直线与抛物线相切,
所以![]() ,
,
解得![]() ,
,
所以直线方程为:![]() 或
或![]() .
.
(2)假设存在点![]() ,设过点
,设过点![]() 的直线方程为:
的直线方程为:![]() ,
,
与![]() .联立得:
.联立得:![]() ,
,
由韦达定理得:![]() ,
,
因为点![]() 到直线
到直线![]() 的距离相等,
的距离相等,
所以![]() 关于x轴对称,
关于x轴对称,
所以![]() ,
,
即![]() ,
,
所以![]() ,
,
即![]() ,
,
解得![]() .
.
所以存在,点![]()

练习册系列答案
相关题目
【题目】在某市高中某学科竞赛中,某一个区4000名考生的参赛成绩统计如图所示.
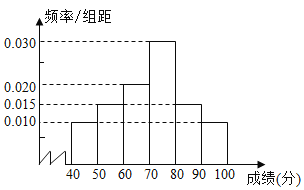
(1)求这4000名考生的竞赛平均成绩![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)记70分以上为优秀,70分及以下为合格,结合频率分布直方图完成下表,并判断是否有99%的把握认为该学科竞赛成绩与性别有关?
合格 | 优秀 | 合计 | |
男生 | 720 |
|
|
女生 |
| 1020 |
|
合计 |
|
| 4000 |
附:
p(k2≥k0) | 0.010 | 0.005 | 0.001 |
k0 | 6.635 | 7.879 | 10.828 |
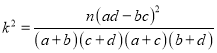 .
.