题目内容
| |||||||||||||||
答案:C

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
| |||||
| |||||
若集合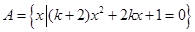 有且仅有2个子集,则实数
有且仅有2个子集,则实数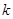 的值是 ( )
的值是 ( )
| A.-2 | B.-2或-1 | C.2或-1 | D. 2或-1 2或-1 |
集合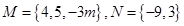 ,若
,若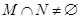 ,则实数
,则实数 的值为( )
的值为( )
A.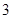 或 或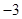 | B.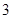 | C.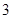 或 或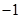 | D.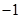 |
题目内容
| |||||||||||||||

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
| |||||
| |||||
若集合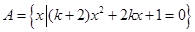 有且仅有2个子集,则实数
有且仅有2个子集,则实数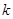 的值是 ( )
的值是 ( )
| A.-2 | B.-2或-1 | C.2或-1 | D. 2或-1 2或-1 |
集合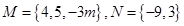 ,若
,若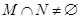 ,则实数
,则实数 的值为( )
的值为( )
A.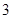 或 或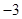 | B.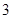 | C.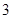 或 或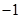 | D.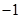 |