题目内容
已知函数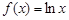 ,
,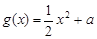 (
(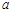 为常数),直线
为常数),直线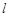 与函数
与函数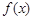 、
、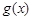 的图象都相切,且
的图象都相切,且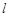 与函数
与函数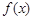 图象的切点的横坐标为
图象的切点的横坐标为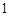 .
.
(1)求直线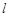 的方程及
的方程及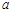 的值;
的值;
(2)若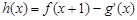 [注:
[注: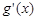 是
是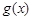 的导函数],求函数
的导函数],求函数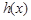 的单调递增区间;
的单调递增区间;
(3)当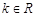 时,试讨论方程
时,试讨论方程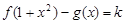 的解的个数.
的解的个数.
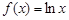 ,
,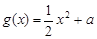 (
(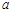 为常数),直线
为常数),直线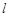 与函数
与函数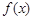 、
、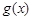 的图象都相切,且
的图象都相切,且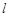 与函数
与函数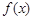 图象的切点的横坐标为
图象的切点的横坐标为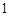 .
.(1)求直线
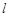 的方程及
的方程及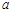 的值;
的值;(2)若
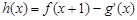 [注:
[注: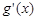 是
是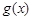 的导函数],求函数
的导函数],求函数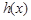 的单调递增区间;
的单调递增区间;(3)当
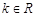 时,试讨论方程
时,试讨论方程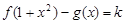 的解的个数.
的解的个数.(1) 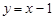 ;
; 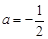 ;(2)
;(2) 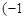 ,
,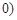 ;(3)详见解析.
;(3)详见解析.
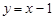 ;
; 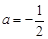 ;(2)
;(2) 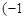 ,
,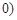 ;(3)详见解析.
;(3)详见解析.试题分析:(1)利用函数在
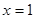 处的导数,等于在
处的导数,等于在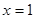 处切线的斜率,所以先求
处切线的斜率,所以先求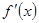 ,再求
,再求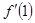 ,直线
,直线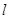 的斜率就是
的斜率就是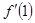 ,直线
,直线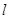 过点
过点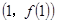 ,代入得到直线
,代入得到直线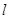 的方程,直线
的方程,直线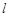 与
与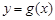 的图象相切,所以代入联立
的图象相切,所以代入联立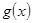 ,
,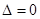 得到
得到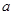 值;(2)先求
值;(2)先求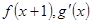 , 得到
, 得到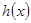 ,再求
,再求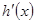 ,令
,令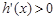 ,得到
,得到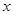 的取值范围,即求得函数
的取值范围,即求得函数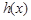 的单调递增区间;(3)令
的单调递增区间;(3)令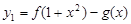
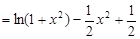 ,
,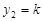 ,再求
,再求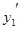 ,得到极值点,然后列表分析当
,得到极值点,然后列表分析当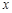 变化时,
变化时,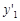 ,
,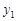 的变化情况,结合
的变化情况,结合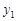 为偶函数,画出
为偶函数,画出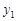 的函数图形,再画
的函数图形,再画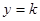 ,当直线
,当直线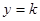 上下变化时,可以看出交点的变化,根据交点的不同,从而确定,再不同
上下变化时,可以看出交点的变化,根据交点的不同,从而确定,再不同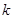 的范围下得到不同的交点个数.此问注意分类讨论思想的使用,不要遗漏情况.属于较难习题.
的范围下得到不同的交点个数.此问注意分类讨论思想的使用,不要遗漏情况.属于较难习题. 试题解析:(1)解:由
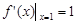 ,
,故直线
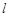 的斜率为
的斜率为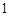 ,切点为
,切点为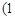 ,
,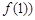 ,即
,即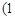 ,
,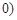 ,
,所以直线
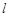 的方程为
的方程为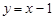 . 3分
. 3分直线
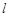 与
与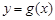 的图象相切,等价于方程组
的图象相切,等价于方程组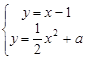 只有一解,
只有一解,即方程
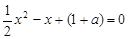 有两个相等实根,
有两个相等实根,所以令
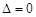 ,解得
,解得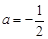 . 5分
. 5分(2)因为
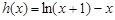
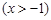 ,
,由
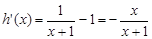 ,
,令
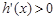 ,所以
,所以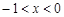 ,
,所以函数
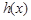 的单调递增区间是
的单调递增区间是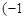 ,
,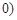 . 8分
. 8分(3)令
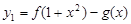
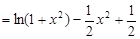 ,
,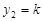 ,
,由
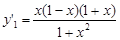 ,令
,令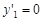 ,得
,得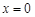 ,
,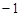 ,
,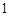 , 10分
, 10分当
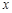 变化时,
变化时,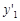 ,
,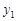 的变化情况如下表:
的变化情况如下表: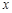 | 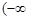 , ,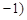 | 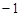 | 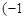 , ,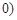 |  | 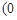 , ,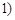 | 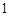 | 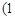 , ,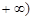 |
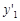 | + |  | - |  | + |  | - |
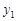 |  | 极大值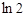 |  | 极小值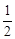 |  | 极大值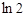 |  |
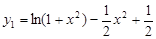 为偶函数, 所以函数
为偶函数, 所以函数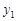 的图象如图:
的图象如图: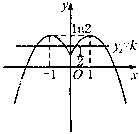
当
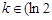 ,
,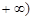 时,方程无解;
时,方程无解;当
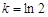 或
或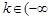 ,
,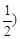 时,方程有两解;
时,方程有两解;当
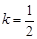 时,方程有三解;
时,方程有三解;当
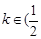 ,
,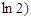 时,方程有四解. 14分
时,方程有四解. 14分
练习册系列答案
相关题目
 .
.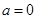 时,求曲线
时,求曲线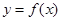 在点
在点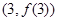 的切线方程;
的切线方程;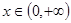 ,
,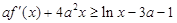 恒成立,求实数
恒成立,求实数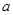 的取值范围;
的取值范围;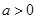 时,试讨论
时,试讨论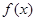 在
在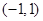 内的极值点的个数.
内的极值点的个数.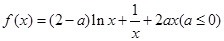 .
.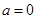 时,求
时,求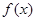 的极值;
的极值;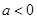 时,讨论
时,讨论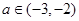 ,
,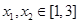 ,恒有
,恒有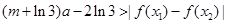 成立,求实数
成立,求实数 的取值范围.
的取值范围.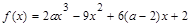 ,
,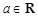 .
.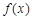 在
在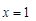 处取得极值,求实数
处取得极值,求实数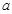 的值;
的值;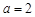 ,求函数
,求函数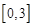 上的最大值和最小值.
上的最大值和最小值.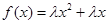 ,
,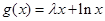 ,
,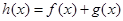 ,其中
,其中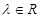 ,且
,且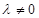 .
.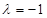 时,求函数
时,求函数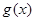 的最大值;
的最大值;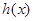 的单调区间;
的单调区间;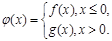 若对任意给定的非零实数
若对任意给定的非零实数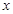 ,存在非零实数
,存在非零实数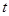 (
(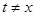 ),使得
),使得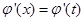 成立,求实数
成立,求实数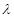 的取值范围.
的取值范围.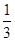 ax3-
ax3- x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.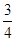 x2-bx+
x2-bx+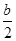 -
-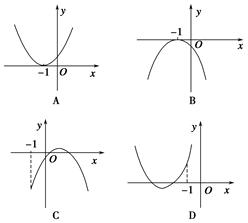
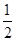 x2+bln (x+2)在(-1,+∞)上是减函数,则b的取值范围是________.
x2+bln (x+2)在(-1,+∞)上是减函数,则b的取值范围是________.