题目内容
已知函数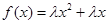 ,
,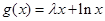 ,
,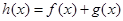 ,其中
,其中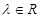 ,且
,且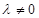 .
.
⑴当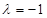 时,求函数
时,求函数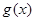 的最大值;
的最大值;
⑵求函数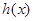 的单调区间;
的单调区间;
⑶设函数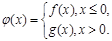 若对任意给定的非零实数
若对任意给定的非零实数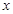 ,存在非零实数
,存在非零实数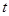 (
(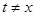 ),使得
),使得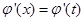 成立,求实数
成立,求实数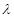 的取值范围.
的取值范围.
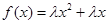 ,
,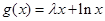 ,
,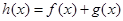 ,其中
,其中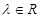 ,且
,且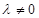 .
.⑴当
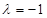 时,求函数
时,求函数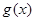 的最大值;
的最大值;⑵求函数
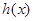 的单调区间;
的单调区间;⑶设函数
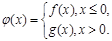 若对任意给定的非零实数
若对任意给定的非零实数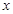 ,存在非零实数
,存在非零实数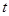 (
(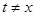 ),使得
),使得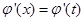 成立,求实数
成立,求实数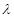 的取值范围.
的取值范围.⑴-1; ⑵详见解析; ⑶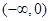
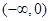
试题分析:⑴令g′(x)=0求出根
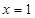 ,判断g′(x)在
,判断g′(x)在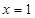 左右两边的符号,得到g(x)在
左右两边的符号,得到g(x)在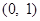 上单调递增,在
上单调递增,在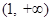 上单调递减,可知g(x)最大值为g(1),并求出最值;
上单调递减,可知g(x)最大值为g(1),并求出最值;⑵解不等式
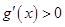 得出函数
得出函数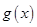 的单调增区间,导数小于零求出单调递减区间,注意单调区间与定义域取交集;
的单调增区间,导数小于零求出单调递减区间,注意单调区间与定义域取交集;⑶不等式恒成立就是求函数的最值,注意对参数的讨论.
试题解析:⑴当
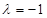 时,
时,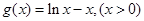 ∴
∴
令
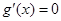 ,则
,则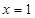 , ∴
, ∴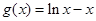 在
在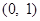 上单调递增,在
上单调递增,在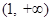 上单调递减
上单调递减∴
 (4分)
(4分)⑵
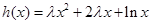 ,
,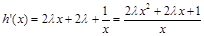 ,(
,(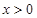 )
)∴当
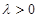 时,
时,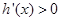 ,∴函数
,∴函数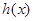 的增区间为
的增区间为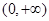 ,
,当
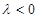 时,
时,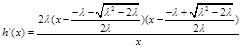 ,
,当
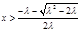 时,
时,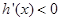 ,函数
,函数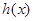 是减函数;当
是减函数;当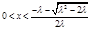 时,
时,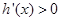 ,函数
,函数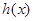 是增函数.
是增函数.综上得,当
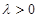 时,
时,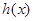 的增区间为
的增区间为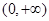 ;
; 当
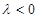 时,
时,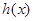 的增区间为
的增区间为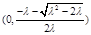 ,减区间为
,减区间为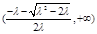 (10分)
(10分)⑶当
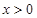 ,
,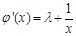 在
在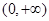 上是减函数,此时
上是减函数,此时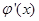 的取值集合
的取值集合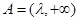 ;
;当
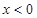 时,
时, ,
,若
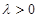 时,
时,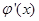 在
在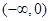 上是增函数,此时
上是增函数,此时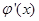 的取值集合
的取值集合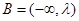 ;
;若
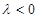 时,
时,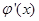 在
在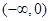 上是减函数,此时
上是减函数,此时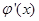 的取值集合
的取值集合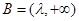 .
.对任意给定的非零实数
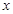 ,
,①当
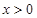 时,∵
时,∵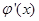 在
在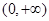 上是减函数,则在
上是减函数,则在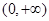 上不存在实数
上不存在实数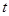 (
(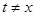 ),使得
),使得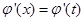 ,则
,则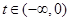 ,要在
,要在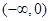 上存在非零实数
上存在非零实数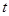 (
(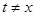 ),使得
),使得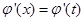 成立,必定有
成立,必定有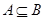 ,∴
,∴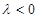 ;
;②当
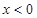 时,
时, 在
在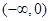 时是单调函数,则
时是单调函数,则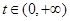 ,要在
,要在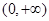 上存在非零实数
上存在非零实数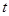 (
(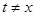 ),使得
),使得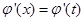 成立,必定有
成立,必定有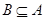 ,∴
,∴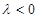 .
.综上得,实数
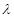 的取值范围为
的取值范围为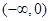 . (14分).
. (14分).
练习册系列答案
相关题目
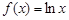 ,
,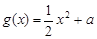 (
(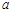 为常数),直线
为常数),直线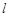 与函数
与函数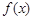 、
、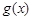 的图象都相切,且
的图象都相切,且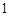 .
.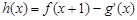 [注:
[注: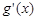 是
是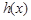 的单调递增区间;
的单调递增区间;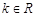 时,试讨论方程
时,试讨论方程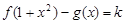 的解的个数.
的解的个数.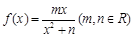 , 在
, 在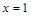 处取得极小值2.
处取得极小值2.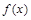 的解析式;
的解析式;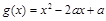 , 若对于任意
, 若对于任意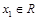 ,总存在
,总存在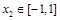 , 使得
, 使得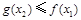 , 求实数
, 求实数 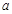 的取值范围.
的取值范围.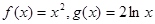 .
.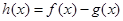 ,求
,求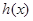 的最小值;
的最小值;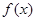 的图象,使得
的图象,使得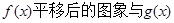 的图象有公共点且在公共点处切线相同.
的图象有公共点且在公共点处切线相同.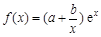 .
.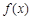 在(0,+∞)内的极值;
在(0,+∞)内的极值;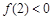 ,
,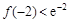 ,且
,且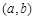 形成的平面区域的面积.
形成的平面区域的面积.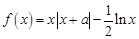 .
.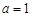 ,求
,求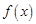 在点
在点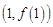 处的切线方程;
处的切线方程;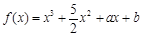 (
(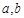 为常数),其图象是曲线
为常数),其图象是曲线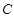 .
.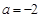 时,求函数
时,求函数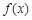 的单调减区间;
的单调减区间;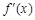 ,若存在唯一的实数
,若存在唯一的实数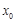 ,使得
,使得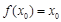 与
与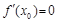 同时成立,求实数
同时成立,求实数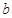 的取值范围;
的取值范围;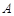 为曲线
为曲线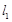 与曲线
与曲线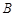 ,在点
,在点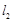 ,设切线
,设切线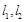 的斜率分别为
的斜率分别为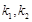 .问:是否存在常数
.问:是否存在常数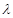 ,使得
,使得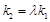 ?若存在,求出
?若存在,求出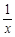 -(2+a)lnx(a≥0)
-(2+a)lnx(a≥0) 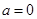 时,求
时,求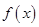 的极值;
的极值;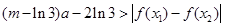 成立,求实数m的取值范围。
成立,求实数m的取值范围。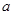 为常数,函数
为常数,函数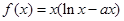 有两个极值点
有两个极值点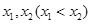 ,则( )
,则( )