题目内容
定义在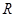 上的奇函数
上的奇函数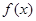 ,当
,当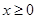 时,
时,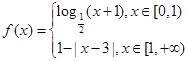 ,则关于
,则关于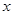 的函数
的函数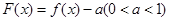 的所有零点之和为( )
的所有零点之和为( )
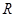 上的奇函数
上的奇函数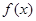 ,当
,当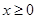 时,
时,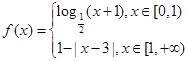 ,则关于
,则关于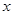 的函数
的函数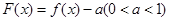 的所有零点之和为( )
的所有零点之和为( )A.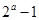 | B.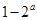 | C.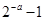 | D.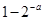 |
D
分析:函数F(x)=f(x)-a(0<a<1)的零点转化为:在同一坐标系内y=f(x),y=a的图象交点的横坐标.作出两函数图象,考查交点个数,结合方程思想,及零点的对称性,为计算提供简便.
解答:解:当-1≤x<0时?1≥-x>0,x≤-1?-x≥1,又f(x)为奇函数∴x<0时,
f(x)=-f(-x)=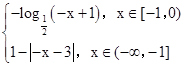
画出y=f(x)和y=a(0<a<1)的图象,
如图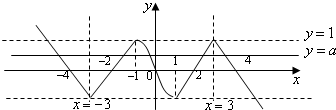
共有5个交点,设其横坐标从左到右分别为x1,x2,x3,x4,x5,则
 =-3,
=-3,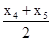 =3,而-log
=3,而-log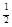 (-x3+1)=a?log2(1-x3)=a?x3=1-2a,
(-x3+1)=a?log2(1-x3)=a?x3=1-2a,
可得x1+x2+x3+x4+x5=1-2a,
故选D.
解答:解:当-1≤x<0时?1≥-x>0,x≤-1?-x≥1,又f(x)为奇函数∴x<0时,
f(x)=-f(-x)=
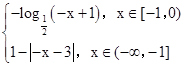
画出y=f(x)和y=a(0<a<1)的图象,
如图

共有5个交点,设其横坐标从左到右分别为x1,x2,x3,x4,x5,则
 =-3,
=-3,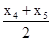 =3,而-log
=3,而-log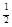 (-x3+1)=a?log2(1-x3)=a?x3=1-2a,
(-x3+1)=a?log2(1-x3)=a?x3=1-2a,可得x1+x2+x3+x4+x5=1-2a,
故选D.

练习册系列答案
相关题目
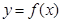 是定义在R上的奇函数,当
是定义在R上的奇函数,当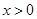 时,
时,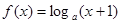 (其中
(其中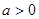 且
且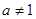 )
)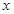 为何值时,
为何值时,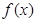 的值的小于0?
的值的小于0?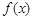 的定义域为
的定义域为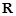 ,
,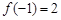 ,对任意
,对任意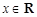 ,
,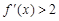 ,则
,则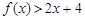 的解集为( )
的解集为( )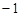 ,1)
,1)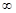 )
)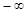 ,
,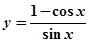 为( )
为( )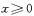 时,
时,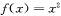 ,若对任意的
,若对任意的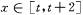 ,不等式
,不等式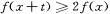 恒成立,则实数t的取值范围是. _______
恒成立,则实数t的取值范围是. _______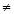 1,F(x)为偶函数,则G(x)=F(x)·log
1,F(x)为偶函数,则G(x)=F(x)·log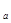 (x+
(x+ )是_______函数(填“奇”或“偶”),它的图像关于______对称。
)是_______函数(填“奇”或“偶”),它的图像关于______对称。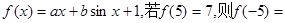

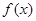 的奇偶性并给予证明;
的奇偶性并给予证明;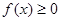 的实数
的实数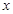 的取值范围。
的取值范围。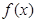 是定义在
是定义在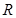 上的奇函数,当
上的奇函数,当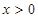 时,
时,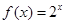 ,则
,则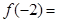 ___________.
___________.