题目内容
【题目】
、
满足约束条件
，若
取得最大值的最优解不唯一，则实数
的值为__________．
【答案】
或
【解析】
由题意作出已知条件的平面区域，将
化为
，
为直线在
轴上的截距，然后对直线与三条边界直线的斜率分别相等进行分类讨论，利用数形结合思想可求得实数
的值.
作出不等式组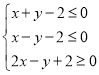
所表示的可行域如下图所示：
将化为，为直线在轴上的截距.
①当直线与直线
的斜率相等时，即当
时，
平移直线，可知当直线与直线重合时，直线在轴上的截距最大，合乎题意；
②当直线与直线
的斜率相等时，即当
时，
平移直线，可知当直线过点
时，直线在轴上的截距最大，不合乎题意；
③当直线与直线
的斜率相等时，即当
时，
平移直线，可知当直线与直线重合时，直线在轴上的截距最大，合乎题意.
综上所述，或.
故答案为：或.
练习册系列答案
考前必练系列答案
相关题目
