题目内容
【题目】(10分)设![]() 和
和![]() 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量![]() 表示方程
表示方程
![]() 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(Ⅰ)求方程![]() 有实根的概率;
有实根的概率;
(Ⅱ)求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)求在先后两次出现的点数中有5的条件下,方程![]() 有实根的概率.
有实根的概率.
【答案】(Ⅰ)![]()
(Ⅱ)
![]()
(Ⅲ)![]()
【解析】本试题主要考查了古典概型概率的计算,以及分布列和数学期望的求解的综合运用。
(1)中理解本题是一个等可能事件的概率,试验发生包含的基本事件总数为6×6=36,那么借助于使方程有实根△=b2-4c≥0,得到事件A发生的基本事件数,得到概率值。
(2)利用ξ=0,1,2的可能取值,分别得到各个取值的概率值,然后写出分布列和数学期望值
(3)分析在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根,这是一个条件概率,利用条件概率公式得到结论。
解:(I)由题意知,本题是一个等可能事件的概率,
试验发生包含的基本事件总数为6×6=36,
满足条件的事件是使方程有实根,则△=b2-4c≥0,即.
下面针对于c的取值进行讨论
当c=1时,b=2,3,4,5,6; 当c=2时,b=3,4,5,6;
当c=3时,b=4,5,6; 当c=4时,b=4,5,6;
当c=5时,b=5,6; 当c=6时,b=5,6,
目标事件个数为5+4+3+3+2+2=19,
因此方程![]() 有实根的概率为
有实根的概率为![]()
(II)由题意知用随机变量ξ表示方程![]() 实根的个数得到
实根的个数得到
ξ=0,1,2 根据第一问做出的结果得到
则![]() ,
,![]() ,
,![]() ,
,
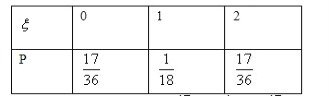
∴ξ的分布列为

∴ξ的数学期望 ![]()
(III)在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根,
这是一个条件概率,
记“先后两次出现的点数中有5”为事件M,
“方程![]() 有实根”为事件N,
有实根”为事件N,
则,![]() ,
,![]() ∴
∴![]()

练习册系列答案
相关题目