题目内容
18.已知函数f(x)=ax2-(3a+1)x+2a+1(a∈R).(1)若f(x)≤0恒成立,试求a的值;
(2)解关于x的不等式f(x)<0.
分析 (1)当a=0时,易知f(x)=-x+1,再讨论当a≠0时可得$\left\{\begin{array}{l}{a<0}\\{△=(3a+1)^{2}-4a(2a+1)≤0}\end{array}\right.$,从而解得;
(2)化简不等式[ax-(2a+1)](x-1)<0,从而分类讨论以求解不等式即可.
解答 解:(1)当a=0时,f(x)=-x+1,f(x)≤0不可能恒成立;
当a≠0时,
$\left\{\begin{array}{l}{a<0}\\{△=(3a+1)^{2}-4a(2a+1)≤0}\end{array}\right.$,
解得,a=-1.
(2)∵f(x)=ax2-(3a+1)x+2a+1<0,
∴[ax-(2a+1)](x-1)<0,
当a<-1时,$\frac{2a+1}{a}$>1,
故不等式的解集为$(-∞,1)∪(\frac{2a+1}{a},+∞)$;
当a=-1时,
故不等式的解集为{x|x≠1};
当-1<a<0时,$\frac{2a+1}{a}$<1,
故不等式的解集为$(-∞,\frac{2a+1}{a})∪(1,+∞)$;
当a=0时,
不等式的解集为(1,+∞);
当a>0时,$\frac{2a+1}{a}$>1;
故不等式的解集为$({1,\frac{2a+1}{a}})$.
点评 本题考查了恒成立问题与二次函数的性质的应用,同时考查了分类讨论的思想应用,难点在于分类讨论的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知i为虚数单位,则z•(1+i)=3-i,则复数z等于( )
| A. | 2-2i | B. | 2+2i | C. | 1-2i | D. | 1+2i |
3.已知集合A={-2,-1,0,1,2},B={x|-2<x<1},则A∩B=( )
| A. | {-1,0} | B. | {0,1} | C. | {-1,0,1} | D. | {0,1,2} |
10.某工人生产合格零售的产量逐月增长,前5个月的产量如表所示:
(I)若从这5组数据中抽出两组,求抽出的2组数据恰好是相邻的两个月数据的概率;
(Ⅱ)请根据所给5组数据,求出 y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;并根据线性回归方程预测该工人第6个月生产的合格零件的件数.
(附:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 合格零件y(件) | 50 | 60 | 70 | 80 | 100 |
(Ⅱ)请根据所给5组数据,求出 y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;并根据线性回归方程预测该工人第6个月生产的合格零件的件数.
(附:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
8.某办公室刚装修一新,放些植物花草可以清除异味,公司提供绿萝、文竹、碧玉、芦荟4种植物供员工选择,每个员工只能任意选择1种,则员工甲和乙选择的植物不同的概率为( )
| A. | $\frac{7}{16}$ | B. | $\frac{9}{16}$ | C. | $\frac{3}{4}$ | D. | $\frac{13}{16}$ |
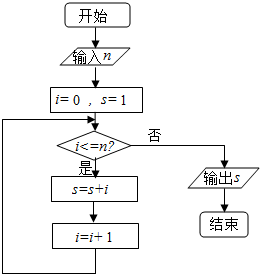 执行如图所示的程序框图,若输入自然数n的值为6,则输出s的值是22.
执行如图所示的程序框图,若输入自然数n的值为6,则输出s的值是22.