题目内容
5.函数f(x)的导数为f′(x),且满足关系式f(x)=x2+3xf′(2)+lnx,则f′(2)的值等于( )| A. | -2 | B. | 2 | C. | $-\frac{9}{4}$ | D. | $\frac{9}{4}$ |
分析 首先对等式两边求导得到关于f'(2)的等式解之.
解答 解:由关系式f(x)=x2+3xf′(2)+lnx,两边求导得f'(x)=2x+3f'(2)+$\frac{1}{x}$,令x=2得f'(2)=4+3f'(2)+$\frac{1}{2}$,解得f'(2)=$-\frac{9}{4}$;
故选C.
点评 本题考查了求导公式的运用;关键是对已知等式两边求导,得到关于f'(x)的等式,对x取2求值.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
15.若动点M(x,y)在运动过程中,总满足关系式$\sqrt{{{(x+5)}^2}+{y^2}}-\sqrt{{{(x-5)}^2}+{y^2}}$=8,则M的轨迹为( )
| A. | 椭圆$\frac{x^2}{25}+\frac{y^2}{16}$=1 | B. | 双曲线$\frac{x^2}{16}-\frac{y^2}{9}$=1的右支 | ||
| C. | 双曲线$\frac{x^2}{9}-\frac{y^2}{16}$=1的右支 | D. | 双曲线$\frac{x^2}{16}-\frac{y^2}{9}$=1的左支 |
 已知空间四边形OABC,如图所示,其对角线为OB,AC.M,N分别为OA,BC的中点,点G在线段MN上,且$\overrightarrow{MG}$=2$\overrightarrow{GN}$,现用基向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$,并设$\overrightarrow{OG}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$,则x+y+z=$\frac{5}{6}$.
已知空间四边形OABC,如图所示,其对角线为OB,AC.M,N分别为OA,BC的中点,点G在线段MN上,且$\overrightarrow{MG}$=2$\overrightarrow{GN}$,现用基向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$,并设$\overrightarrow{OG}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$,则x+y+z=$\frac{5}{6}$.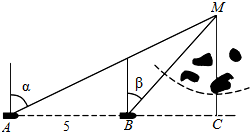 如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.
如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.