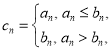题目内容
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2016年1月至2018年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
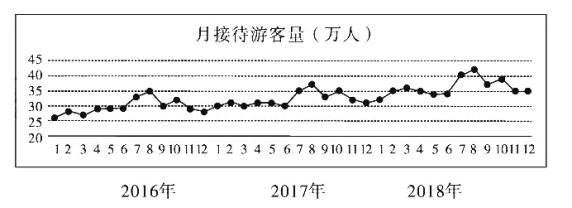
根据该折线图,判断下列结论:
(1)月接待游客量逐月增加;
(2)年接待游客量逐年增加;
(3)各年的月接待游客量高峰期大致在7,8月;
(4)各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳.
其中正确结论的个数为( )
A.1B.2C.3D.4
【答案】C
【解析】
由题图可知逐一分析即可,这三年8月到9月的月接待游客量在减少,则结论(1)错误,(2)(3)(4)正确.
由题图可知,这三年8月到9月的月接待游客量在减少,则结论(1)错误;
年接待游客数量逐年增加,故(2)正确;
各年的月接待游客量高峰期大致在7,8月,故(3)正确;
各年1月至6月的月接待游客量相对变化较小,而7月至12月则变化较大,故(4)正确;
故选:C.

 名校课堂系列答案
名校课堂系列答案【题目】某学校高二年级举行了由全体学生参加的一分钟跳绳比赛,计分规则如下表:
每分钟跳绳个数 |
|
|
|
|
|
得分 | 16 | 17 | 18 | 19 | 20 |
年级组为了解学生的体质,随机抽取了100名学生的跳绳个数作为一个样本,绘制了如下样本频率分布直方图.
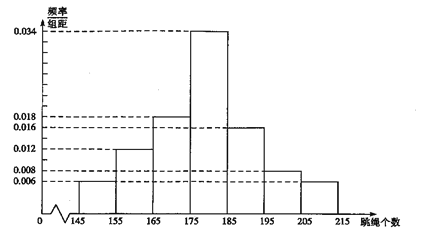
(1)现从样本的100名学生跳绳个数中,任意抽取2人的跳绳个数,求两人得分之和小于35分的概率;(用最简分数表示)
(2)若该校高二年级共有2000名学生,所有学生的一分钟跳绳个数![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() ,
,![]() 为样本平均数的估计值(同一组中数据以这组数据所在区间中点值作代表).利用所得的正态分布模型,解决以下问题:
为样本平均数的估计值(同一组中数据以这组数据所在区间中点值作代表).利用所得的正态分布模型,解决以下问题:
(i)估计每分钟跳绳164个以上的人数(结果四舍五入到整数);
(ii)若在全年级所有学生中随机抽取3人,每分钟跳绳在179个以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望与方差.
的分布列和数学期望与方差.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.