题目内容
已知函数f(x)=
,函数g(x)=log2f(x)
(1)求f(x)的定义域;
(2)判断g(x)的奇偶性;
(3)画出函数y=f(x)的图象,并写出图象的对称中心.
| x-1 |
| x+1 |
(1)求f(x)的定义域;
(2)判断g(x)的奇偶性;
(3)画出函数y=f(x)的图象,并写出图象的对称中心.
(1)要使函数f(x)=
有意义,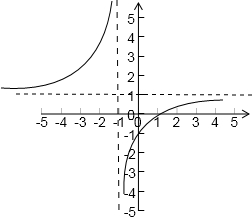
只需x+1≠0,即x≠-1
∴函数定义域为{x∈R|x≠-1}
(2)∵函数g(x)=log2f(x)=log2
由
>0,得-1<x<1,∴函数g(x)的定义域为(-1,1)
∵g(-x)=log2
=loga(
)-1=-log2
=-g(x)
∴f(x)为奇函数
(3)∵f(x)=
=1-
其图象如图
对称中心为(-1,1)
| x-1 |
| x+1 |

只需x+1≠0,即x≠-1
∴函数定义域为{x∈R|x≠-1}
(2)∵函数g(x)=log2f(x)=log2
| 1-x |
| 1+x |
由
| 1-x |
| 1+x |
∵g(-x)=log2
| 1-x |
| 1+x |
| 1+x |
| 1-x |
| 1+x |
| 1-x |
∴f(x)为奇函数
(3)∵f(x)=
| x-1 |
| x+1 |
| 2 |
| x+1 |
其图象如图
对称中心为(-1,1)

练习册系列答案
相关题目
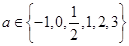 ,则使函数
,则使函数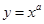 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有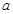 的值有( )
的值有( )