题目内容
已知函数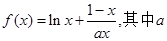 为大于零的常数。
为大于零的常数。
(1)若函数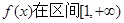 内调递增,求a的取值范围;
内调递增,求a的取值范围;
(2)求函数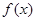 在区间[1,2]上的最小值。
在区间[1,2]上的最小值。
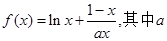 为大于零的常数。
为大于零的常数。(1)若函数
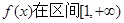 内调递增,求a的取值范围;
内调递增,求a的取值范围;(2)求函数
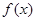 在区间[1,2]上的最小值。
在区间[1,2]上的最小值。(1)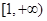 ,(2)①当
,(2)①当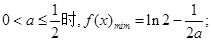
②当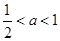 时,
时,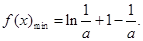
③当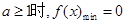
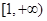 ,(2)①当
,(2)①当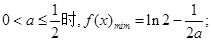
②当
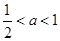 时,
时,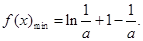
③当
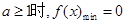
试题分析:
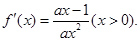 2分
2分(1)由已知,得
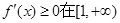 上恒成立, 3分
上恒成立, 3分即
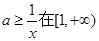 上恒成立, 又
上恒成立, 又 当
当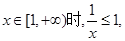 5分
5分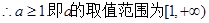 6分
6分(2)①当
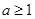 时,
时,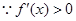 在(1,2)上恒成立, 这时
在(1,2)上恒成立, 这时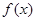 在[1,2]上为增函数
在[1,2]上为增函数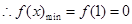 8分
8分②当
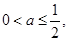
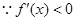 在(1,2)上恒成立, 这时
在(1,2)上恒成立, 这时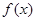 在[1,2]上为减函数
在[1,2]上为减函数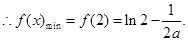 10分
10分③当
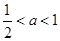 时, 令
时, 令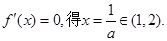
又
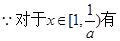
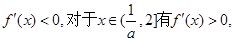
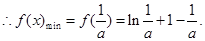 12分
12分综上,
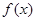 在[1,2]上的最小值为
在[1,2]上的最小值为①当
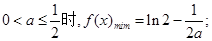
②当
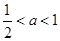 时,
时,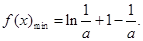
③当
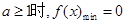 13分
13分点评:对于此类问题要把函数的单调性特征与导数两个知识加以有机会组合.特别,在研究函数的单调区间或决断函数的单调性时,三个基本步骤不可省,一定要在定义域内加以求解单调区间或判断单调性

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
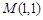 且与曲线
且与曲线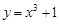 相切的直线方程是( )
相切的直线方程是( )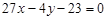
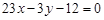 或
或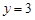
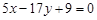
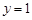
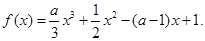
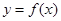 在点
在点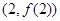 处的切线与直线
处的切线与直线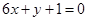 平行,求出这条切线的方程;
平行,求出这条切线的方程;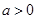 ,讨论函数
,讨论函数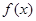 的单调区间;
的单调区间;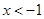 ,恒有
,恒有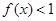 ,求实数
,求实数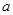 的取值范围.
的取值范围.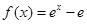 的图象,直线
的图象,直线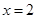 及x轴所围成的阴影部分面积等于( )
及x轴所围成的阴影部分面积等于( )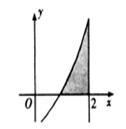
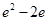
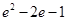
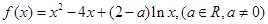
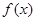 的单调区间;
的单调区间;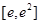 上的最小值.
上的最小值.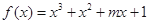 在
在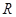 上无极值点,则实数
上无极值点,则实数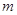 的取值范围是_________.
的取值范围是_________.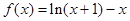 的单调递减区间为 ;
的单调递减区间为 ;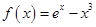 ,
,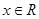 ,则函数的极值点的个数是( )
,则函数的极值点的个数是( )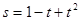 其中
其中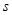 的单位是米,
的单位是米,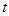 的单位是秒,那么物体在
的单位是秒,那么物体在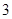 秒末的瞬时速度是( )
秒末的瞬时速度是( ) 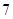 米/秒
米/秒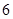 米/秒
米/秒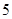 米/秒
米/秒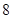 米/秒
米/秒