题目内容
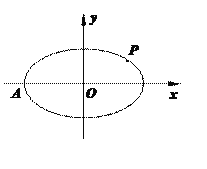
【题目】椭圆![]() 的离心率为
的离心率为![]() , 过点
, 过点![]() , 记椭圆的左顶点为
, 记椭圆的左顶点为![]() .
.
(1)求椭圆的方程;
(2)设垂直于![]() 轴的直线
轴的直线![]() 交椭圆于
交椭圆于![]() 两点, 试求
两点, 试求![]() 面积的最大值;
面积的最大值;
(3)过点![]() 作两条斜率分别为
作两条斜率分别为![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且
两点,且![]() , 求证: 直线
, 求证: 直线![]() 恒过一个定点.
恒过一个定点.
【答案】(1)x2+2y2=1;(2)![]() ;(3)直线BC恒过定点
;(3)直线BC恒过定点![]() .
.
【解析】试题分析:(1)题意列出关于![]() 、
、![]() 、
、![]() 的方程组,结合性质
的方程组,结合性质![]() , 求出
, 求出![]() 、
、![]() 、
、![]() ,即可得结果;(2)设B(m,n),C(-m,n),则S△ABC=
,即可得结果;(2)设B(m,n),C(-m,n),则S△ABC=![]() ×2|m|×|n|=|m|·|n|,根据点
×2|m|×|n|=|m|·|n|,根据点![]() 在椭圆上与基本不等式可得结果;(3)AB:y=k1(x+1),AC:y=k2(x+1),
在椭圆上与基本不等式可得结果;(3)AB:y=k1(x+1),AC:y=k2(x+1),
由![]() 消去y,得(1+2k)x2+4kx+2k-1=0,可得
消去y,得(1+2k)x2+4kx+2k-1=0,可得![]() 的坐标,从而得
的坐标,从而得![]() 的方程,进而可得结果.
的方程,进而可得结果.
试题解析:
(1)由 ,解得
,解得![]()
所以椭圆C的方程为x2+2y2=1.
(2) 解:设B(m,n),C(-m,n),则S△ABC=![]() ×2|m|×|n|=|m|·|n|,
×2|m|×|n|=|m|·|n|,
又1=m2+2n2≥2![]() =2
=2![]() |m|·|n|,所以|m|·|n|≤
|m|·|n|,所以|m|·|n|≤![]() ,
,
当且仅当|m|=![]() |n|时取等号,
|n|时取等号,
从而S△ABC≤![]() ,即△ABC面积的最大值为
,即△ABC面积的最大值为![]() .……………… 8分
.……………… 8分
(3)证明:因为A(-1,0),所以AB:y=k1(x+1),AC:y=k2(x+1),
由![]() 消去y,得(1+2k)x2+4kx+2k-1=0,解得x=-1或
消去y,得(1+2k)x2+4kx+2k-1=0,解得x=-1或![]()
∴ 点![]() ,同理,有
,同理,有![]() ,而k1k2=2,
,而k1k2=2,
∴ ![]()
∴ 直线BC的方程为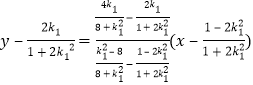
即![]() ,即
,即![]() ,
,
所以,得直线BC恒过定点![]() .
.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案【题目】几个月前,成都街头开始兴起“mobike”、“ofo”等共享单车,这样的共享单车为很多市民解决了最后一公里的出行难题.然而,这种模式也遇到了一些让人尴尬的问题,比如乱停乱放,或将共享单车占为“私有”等.
为此,某机构就是否支持发展共享单车随机调查了50人,他们年龄的分布及支持发展共享单车的人数统计如下表:
年龄 |
|
|
|
|
|
|
受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
支持发展 共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系;
列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系;
年龄低于35岁 | 年龄不低于35岁 | 合计 | |
支持 | |||
不支持 | |||
合计 |
(Ⅱ)若对年龄在![]() ,
,![]() 的被调查人中各随机选取两人进行调查,记选中的4人中支持发展共享单车的人数为
的被调查人中各随机选取两人进行调查,记选中的4人中支持发展共享单车的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.