题目内容

【题目】设椭圆，定义椭圆的“伴随圆”方程为；若抛物线的焦点与椭圆C的一个短轴端点重合，且椭圆C的离心率为．

（1）求椭圆C的方程和“伴随圆”E的方程；

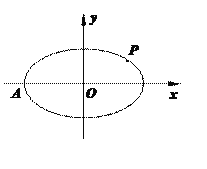
（2）过“伴随圆”E上任意一点P作椭圆C的两条切线PA，PB，A，B为切点，延长PA与“伴随圆”E交于点Q，O为坐标原点．

(i)证明：PA⊥PB；

(ii)若直线OP，OQ的斜率存在，设其分别为，试判断是否为定值，若是， 求出该值；若不是，请说明理由．

【答案】（1） （2）(i)见解析，(ii)

【解析】试题分析：（1）先求抛物线焦点得，再由离心率求，最后写出椭圆标准方程及“伴随圆”方程（2）(i)联立切线方程与椭圆方程，利用判别式为零得，根据点P在“伴随圆”上得关于k的一元二次方程，利用韦达定理得，即得结论，(ii) 由切线方程与圆方程联立，结合韦达定理得 ，再根据斜率公式化简得定值

试题解析：（1）由题意得

（2）(i)设 ，切线方程为 ，与椭圆方程联立得 ，由 得

把代入得 ，因此

当切线斜率不存在或等于零时，结论也成立

(ii)由切线方程与圆方程联立得，

所以 ，当切线斜率不存在时，结论也成立

练习册系列答案
相关题目

【题目】已知函数fn（x）= x3﹣ （n+1）x2+x（n∈N*），数列{an}满足an+1=f'n（an），a1=3．
（1）求a2 ， a3 ， a4；
（2）根据（1）猜想数列{an}的通项公式，并用数学归纳法证明；
（3）求证： + +…+ ＜ ．

【题目】已知曲线C的参数方程是 （α为参数），直线l的参数方程为 （t为参数），
（1）求曲线C与直线l的普通方程；
（2）若直线l与曲线C相交于P，Q两点，且|PQ|= ，求实数m的值．

【题目】设函数f（x）=x2﹣2tx+2，其中 t∈R．
（1）若t=1，求函数f（x）在区间[0，4]上的取值范围；
（2）若t=1，且对任意的x∈[a，a+2]，都有f（x）＜5，求实数a的取值范围；
（3）若对任意的x1 ， x2∈[0，4]，都有f（x1）﹣f（x2）≤8，求t的取值范围．

【题目】定义：分子为1且分母为正整数的分数叫做单位分数，我们可以把1拆分成多个不同的单位分数之和．例如：1= + + ，1= + + + ，1= + + + + ，…，依此拆分法可得1= + + + + + + + + + + + + + ，其中m，n∈N* ， 则m﹣n=（ ）
A.﹣2
B.﹣4
C.﹣6
D.﹣8

【题目】已知 a∈R，函数 f（x）=a﹣ ．
（1）证明：f（x）在（﹣∞，+∞）上单调递增；
（2）若f（x）为奇函数，求：
①a的值；
②f（x）的值域．

【题目】集合A= ，若BA求m的取值范围．

【题目】已知点P（﹣1，4）及圆C：（x﹣2）2+（y﹣3）2=1．则下列判断正确的序号为 ．
①点P在圆C内部；
②过点P做直线l，若l将圆C平分，则l的方程为x+3y﹣11=0；
③过点P做直线l与圆C相切，则l的方程为y﹣4=0或3x+4y﹣13=0；
④一束光线从点P出发，经x轴反射到圆C上的最短路程为 ．

【题目】椭圆的离心率为, 过点, 记椭圆的左顶点为.

（1）求椭圆的方程；

（2）设垂直于轴的直线交椭圆于两点, 试求面积的最大值；

（3）过点作两条斜率分别为的直线交椭圆于两点，且, 求证: 直线恒过一个定点.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网