题目内容
【题目】已知数列{an}满足a1+a2+…+an=an+1﹣2.
(1)若a1=2,求数列{an}的通项公式;
(2)若数列1,a2,a4,b1,b2,…bn,…成等差数列,求数列{bn}的前n项和为Sn.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)Sn=an+1﹣2,计算得到Sn=an+1﹣2,根据等比数列公式计算得到答案.
(2)根据1,a2,a4成等差数列,得到a2![]() ,得到数列{bn}是首项为
,得到数列{bn}是首项为![]() ,公差为
,公差为![]() 的等差数列,计算得到答案.
的等差数列,计算得到答案.
(1)由题意,可知Sn=an+1﹣2,则a2=S1+2=a1+2=4.
当n≥2时,an=Sn﹣Sn﹣1=an+1﹣2﹣(an﹣2),整理,得an+1=2an,
![]() 时,满足
时,满足![]() .
.
∴数列{an}是以2为首项,2为公比的等比数列,∴an=2n,n∈N*.
(2)由题意,可知a1=a2﹣2,
∵a1+a2=a3﹣2,∴a3=a1+a2+2=a2﹣2+a2+2=2a2.
∵1,a2,a4成等差数列,∴2a2=a4+1,即a4=2a2﹣1.
∵a1+a2+a3=a4﹣2,∴a2﹣2+a2+2a2=2a2﹣1﹣2,解得a2![]() .
.
设等差数列的公差为d,则d=a2﹣1![]() 1
1![]() .
.
∴b1=1![]() (4﹣1)
(4﹣1)![]() .
.
∴数列{bn}是首项为![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
∴Sn![]() (
(![]() )
)![]() n2
n2![]() n.
n.

【题目】2019年全国“两会”,即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国委员会第二次会议,分别于2019年3月5日和3月3日在北京召开.为了了解哪些人更关注“两会”,某机构随机抽取了年龄在![]() 岁之间的200人进行调查.并按年龄绘制的频率分布直方图如图所示,把年龄落在区间
岁之间的200人进行调查.并按年龄绘制的频率分布直方图如图所示,把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年人”和“中老年人”
内的人分别称为“青少年人”和“中老年人”![]() 经统计“青少年人”和“中老年人”的人数之比为
经统计“青少年人”和“中老年人”的人数之比为![]() ,其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是
,其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是![]() .
.
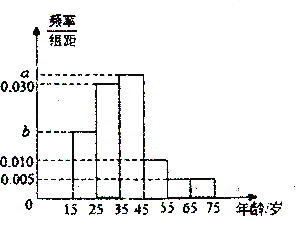
(1)求图中a,b的值;
(2)现采用分层抽样在![]() 和
和![]() 中随机抽取8名代表,从8人中任选2人,求2人中至少有1个是“中老年人”的概率是多少?
中随机抽取8名代表,从8人中任选2人,求2人中至少有1个是“中老年人”的概率是多少?
(3)根据已知条件,完成下面的![]() 列联表,并根据此统计结果判断:能否有
列联表,并根据此统计结果判断:能否有![]() 的把握认为“中老年人”比“青少年人”更加关注“两会”?
的把握认为“中老年人”比“青少年人”更加关注“两会”?
关注 | 不关注 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
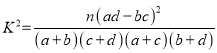
P(K2≥k0) | 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.现统计得到相关统计情况如下:
内,则为合格品,否则为不合格品.现统计得到相关统计情况如下:
甲套设备的样本的频率分布直方图
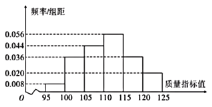
乙套设备的样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 | 1 | 6 | 19 | 18 | 5 | 1 |
(1)根据上述所得统计数据,计算产品合格率,并对两套设备的优劣进行比较;
(2)填写下面列联表,并根据列联表判断是否有95%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:
| 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式: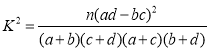 ,其中
,其中![]()