题目内容
【题目】如图1,![]() 与
与![]() 是处在同-个平面内的两个全等的直角三角形,
是处在同-个平面内的两个全等的直角三角形,![]()
![]() ,
,![]() ,连接是
,连接是![]() 边
边![]() 上一点,过
上一点,过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,沿
,沿![]() 将
将![]() 向上翻折,得到如图2所示的六面体
向上翻折,得到如图2所示的六面体![]()
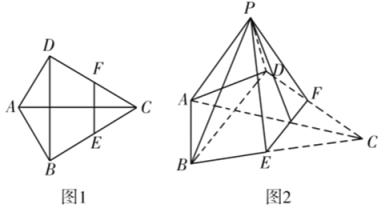
(1)求证:![]()
(2)设![]() 若平面
若平面![]() 底面
底面![]() ,若平面
,若平面![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() ,求
,求![]() 的值;
的值;
(3)若平面![]() 底面
底面![]() ,求六面体
,求六面体![]() 的体积的最大值.
的体积的最大值.
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】
![]() 根据折叠图形,
根据折叠图形, ![]() ,
,![]() 由线面垂直的判定定理可得
由线面垂直的判定定理可得![]() 平面
平面![]() ,再根据
,再根据![]() 平面
平面![]() ,得到
,得到![]() .
.
(2)根据![]()
![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴建立空间直角坐标系,根据
轴建立空间直角坐标系,根据![]() ,
,![]() 可知,
可知,![]() ,表示相应点的坐标,分别求得平面
,表示相应点的坐标,分别求得平面![]() 与平面
与平面![]() 的法向量,代入
的法向量,代入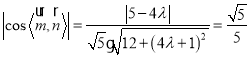 求解.
求解.
![]() 设所求几何体的体积为
设所求几何体的体积为![]() ,设
,设![]() 为高,则
为高,则![]() ,表示梯形BEFD和
,表示梯形BEFD和![]() ABD的面积由
ABD的面积由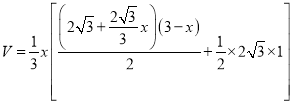
![]() ,再利用导数求最值.
,再利用导数求最值.
(1)证明:不妨设![]() 与
与![]() 的交点为
的交点为![]() 与
与![]() 的交点为
的交点为![]()
由题知,![]() ,则有
,则有![]()
又![]() ,则有
,则有![]()
由折叠可知![]() 所以可证
所以可证![]()
由![]() 平面
平面![]() 平面
平面![]() ,
,
则有![]() 平面
平面![]()
又因为![]() 平面
平面![]() ,
,
所以![]() ....
....
(2)解:依题意,有![]() 平面
平面![]() 平
平![]() 面,
面,
又![]() 平面
平面![]() ,
,
则有![]() 平面
平面![]() ,
,![]() ,又由题意知,
,又由题意知,![]()
如图所示:
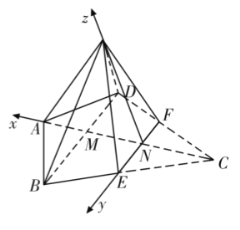
以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系
由题意知![]()
由![]() 可知,
可知,
![]()
则![]()
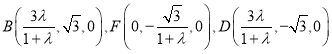
则有![]() ,
,![]()
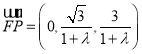 ,
,![]()
设平面![]() 与平面
与平面![]() 的法向量分别为
的法向量分别为![]()
则有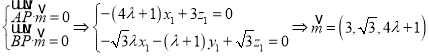
则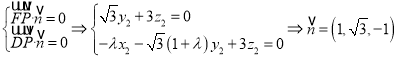
所以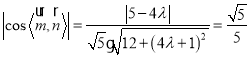
因为![]() ,解得
,解得![]()
![]() 设所求几何体的体积为
设所求几何体的体积为![]() ,设
,设![]() ,
,
则![]() ,
,
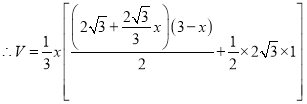

![]()
![]()
![]()
![]() 当
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
![]() 在
在![]() 是增函数,在
是增函数,在![]() 上是减函数
上是减函数
![]() 当
当![]() 时,
时,![]() 有最大值,
有最大值,
即![]()
![]() 六面体
六面体![]() 的体积的最大值是
的体积的最大值是![]()

 阅读快车系列答案
阅读快车系列答案【题目】假如你的公司计划购买台机器,该种机器使用三年后即被淘汰,在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元,在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费,现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记![]() 表示1台机器在三年使用期内的维修次数,
表示1台机器在三年使用期内的维修次数,![]() 表示1台机器在维修上所需的费用(单位:元),
表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式.
的函数解析式.
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求
”的频率不小于0.8,求![]() 的值.
的值.
(3)假设这100台机器在购机的同时每台都购买10次维修服务,或每台都购买11次维修服务,分别计算这100台机器在维修上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买10次还是11次维修服务?
【题目】健身馆某项目收费标准为每次60元,现推出会员优惠活动:具体收费标准如下:
消费次数 | 第1次 | 第2次 | 第3次 | 不少于4次 |
收费比例 | 0.95 | 0.90 | 0.85 | 0.80 |
现随机抽取了100位会员统计它们的消费次数,得到数据如下:
消费次数 | 1次 | 2次 | 3次 | 不少于4次 |
频数 | 60 | 25 | 10 | 5 |
假设该项目的成本为每次30元,根据给出的数据回答下列问题:
(1)估计1位会员至少消费两次的概率
(2)某会员消费4次,求这4次消费获得的平均利润;