题目内容
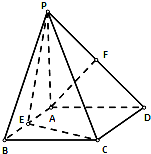 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E、F分别为棱AB、PD的中点.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E、F分别为棱AB、PD的中点.(1)求证:AF⊥平面PCD;
(2)求证:平面PCE⊥平面PCD.
考点:平面与平面垂直的判定,直线与平面垂直的判定
专题:证明题,空间位置关系与距离
分析:(1)由已知可先证明AF⊥PC,由于CD⊥AD,PA⊥CD,且PA∩AD=A,可证CD⊥平面PAD,由AF?平面PAD,从而证明CD⊥AF,又CD∩PD=D,故有AF⊥平面PCD.
(2)取PC的中点G,连接EG,GF,可证EG∥AF,有AF⊥平面PCD,又EG⊥平面PCD,又EG?平面PCE,故可证平面PCE⊥平面PCD.
(2)取PC的中点G,连接EG,GF,可证EG∥AF,有AF⊥平面PCD,又EG⊥平面PCD,又EG?平面PCE,故可证平面PCE⊥平面PCD.
解答:
证明:(1)∵PA⊥底面ABCD,AD,CD?底面ABCD,PA⊥AD,PA⊥CD
又∠PDA=45°,∴△PAD为等腰三角形,∵F是FD的中点,∴AF⊥PC…2分
∵CD⊥AD,PA⊥CD,且PA∩AD=A,∴CD⊥平面PAD
又AF?平面PAD,∴CD⊥AF,
又CD∩PD=D,∴AF⊥平面PCD…5分
(2)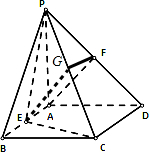
取PC的中点G,连接EG,GF…8分
∵E为AB的中点,∴EA∥CD且EA=
CD
∵F为PD的中点,∴GF∥CD且GF=
CD
∴EA∥GF且GF=EA,∴四边形AEGF是平行四边形…10分
∴EG∥AF,∵AF⊥平面PCD
∴EG⊥平面PCD,又EG?平面PCE
∴平面PCE⊥平面PCD…12分
又∠PDA=45°,∴△PAD为等腰三角形,∵F是FD的中点,∴AF⊥PC…2分
∵CD⊥AD,PA⊥CD,且PA∩AD=A,∴CD⊥平面PAD
又AF?平面PAD,∴CD⊥AF,
又CD∩PD=D,∴AF⊥平面PCD…5分
(2)

取PC的中点G,连接EG,GF…8分
∵E为AB的中点,∴EA∥CD且EA=
| 1 |
| 2 |
∵F为PD的中点,∴GF∥CD且GF=
| 1 |
| 2 |
∴EA∥GF且GF=EA,∴四边形AEGF是平行四边形…10分
∴EG∥AF,∵AF⊥平面PCD
∴EG⊥平面PCD,又EG?平面PCE
∴平面PCE⊥平面PCD…12分
点评:本题主要考察了平面与平面垂直的判定,直线与平面垂直的判定,属于基本知识的考查.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:
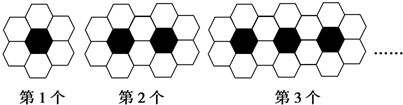
则第n个图案中的白色地面砖有( )

则第n个图案中的白色地面砖有( )
| A、4n-2块 |
| B、4n+2块 |
| C、3n+3块 |
| D、3n-3块 |
 已知等差数列{an}的公差为d,前n项和为Sn,且满足
已知等差数列{an}的公差为d,前n项和为Sn,且满足