题目内容
已知函数f(x)=2x-1+
,则其反函数的解析式为 .
| 1 |
| 2 |
考点:反函数
专题:函数的性质及应用
分析:先由y=2x-1+
解出x,再交换x,y即可.
| 1 |
| 2 |
解答:
解:∵y=2x-1+
,
∴y-
=2x-1,
两边取以2为底的对数得log2(y-
)=x-1,
则x=1+log2(y-
),
交换x,y得y=1+log2(x-
),(x>
),
故答案为:y=1+log2(x-
).
| 1 |
| 2 |
∴y-
| 1 |
| 2 |
两边取以2为底的对数得log2(y-
| 1 |
| 2 |
则x=1+log2(y-
| 1 |
| 2 |
交换x,y得y=1+log2(x-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:y=1+log2(x-
| 1 |
| 2 |
点评:本题考查反函数的求法,利用反函数的定义法求解,属于基础题目.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
化简(tanx+
)cos2x=( )
| 1 |
| tanx |
| A、sinx | ||
| B、tanx | ||
C、
| ||
D、
|
从空间一点P向二面角α-1-β的两个平面作垂线PE,PF,E,F为垂足,若∠EPF=60°,则二面角的平面角的大小为( )
| A、60° | B、120° |
| C、60°或120° | D、不确定 |
动点E在正方体ABCD-A1B1C1D1的棱BC上,F是CD的中点,则二面角C1-EF-C的余弦值的取值范围是( )
A、(0,
| ||||
B、(
| ||||
C、(0,
| ||||
D、(0,
|
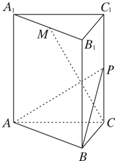 如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2
如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2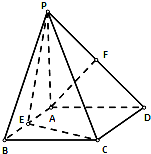 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E、F分别为棱AB、PD的中点.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E、F分别为棱AB、PD的中点.