题目内容
定义:如果函数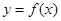 在区间
在区间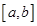 上存在
上存在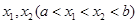 ,满足
,满足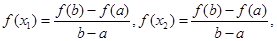 则称函数
则称函数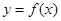 在区间
在区间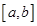 上的一个双中值函数,已知函数
上的一个双中值函数,已知函数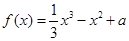 是区间
是区间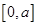 上的双中值函数,则实数
上的双中值函数,则实数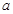 的取值范围是 ( )
的取值范围是 ( )
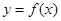 在区间
在区间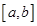 上存在
上存在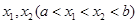 ,满足
,满足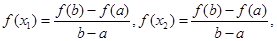 则称函数
则称函数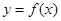 在区间
在区间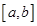 上的一个双中值函数,已知函数
上的一个双中值函数,已知函数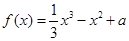 是区间
是区间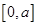 上的双中值函数,则实数
上的双中值函数,则实数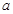 的取值范围是 ( )
的取值范围是 ( )A.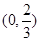 | B.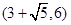 | C.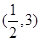 | D.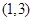 |
B
试题分析:
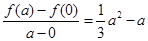 .由题意得:
.由题意得: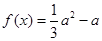 在
在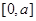 上有两个不同的根.
上有两个不同的根.令
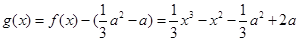 ,则
,则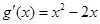 .
.所以
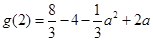 是
是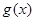 的极小值.
的极小值.所以
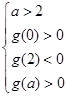
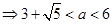 .
.
练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
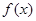 的图象在
的图象在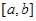 上连续,定义:
上连续,定义: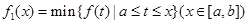 ,
,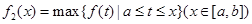 .其中,
.其中,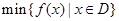 表示函数
表示函数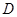 上的最小值,
上的最小值,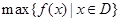 表示函数
表示函数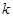 ,使得
,使得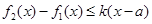 对任意的
对任意的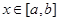 成立,则称函数
成立,则称函数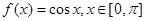 ,试写出
,试写出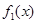 ,
,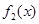 的表达式;
的表达式;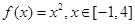 ,试判断
,试判断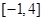 上的“
上的“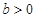 ,函数
,函数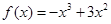 是
是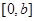 上的2阶收缩函数,求
上的2阶收缩函数,求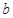 的取值范围.
的取值范围.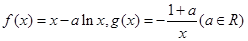 .
. 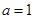 时,求曲线
时,求曲线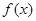 在
在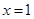 处的切线方程;
处的切线方程;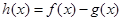 ,求函数
,求函数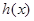 的单调区间;
的单调区间;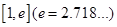 上存在一点
上存在一点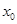 ,使得
,使得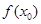 <
<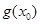 成立,求
成立,求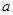 的取值范围.
的取值范围.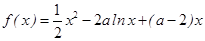
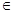 (0,+∞),且x1≠x2,都有
(0,+∞),且x1≠x2,都有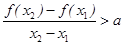 恒成立.若存在,求出a的取值范围;若不存在,说明理由.
恒成立.若存在,求出a的取值范围;若不存在,说明理由.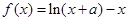 的最大值为0,其中
的最大值为0,其中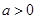 。
。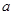 的值;
的值; 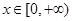 ,有
,有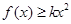 成立,求实数
成立,求实数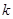 的最大值;
的最大值;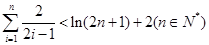
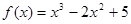 的定义域为区间
的定义域为区间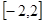 .
.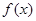 的极大值与极小值;
的极大值与极小值;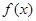 的导函数图象如图所示,若
的导函数图象如图所示,若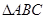 为锐角三角形,则一定成立的是( )
为锐角三角形,则一定成立的是( )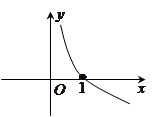
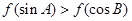
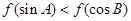
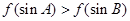
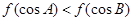
 在点
在点 处的切线方程为________________.
处的切线方程为________________.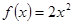 ,则
,则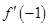 等于 .
等于 .