题目内容
已知函数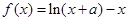 的最大值为0,其中
的最大值为0,其中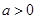 。
。
(1)求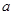 的值;
的值;
(2)若对任意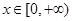 ,有
,有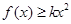 成立,求实数
成立,求实数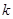 的最大值;
的最大值;
(3)证明: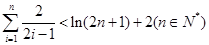
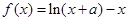 的最大值为0,其中
的最大值为0,其中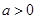 。
。(1)求
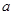 的值;
的值; (2)若对任意
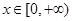 ,有
,有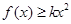 成立,求实数
成立,求实数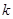 的最大值;
的最大值;(3)证明:
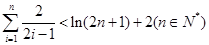
(1)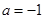 ;(2)
;(2)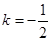 ;(3)详见解析.
;(3)详见解析.
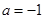 ;(2)
;(2)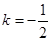 ;(3)详见解析.
;(3)详见解析.试题分析:(1)根据函数的特征可对函数求导,由导数等于零,可求出函数的零点,利用导数与函数单调性的关系:导数大于零,函数在对应区间上单调增,导数小于零,函数在对应区间上单调减,就可用
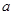 表示出函数的最大值进而求出
表示出函数的最大值进而求出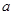 ;(2)先定性分析
;(2)先定性分析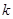 的范围,发现当
的范围,发现当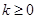 时,易得
时,易得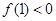 ,即可得出矛盾,进而
,即可得出矛盾,进而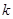 只有小于零,对函数求导后得出导数为零的
只有小于零,对函数求导后得出导数为零的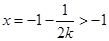 ,再根据
,再根据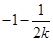 与零的大小关系,可发现
与零的大小关系,可发现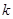 要以
要以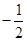 为界进行讨论,又由
为界进行讨论,又由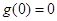 结合函数的单调性不难得出只有
结合函数的单调性不难得出只有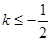 时不等式
时不等式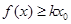 恒成立; (3)当
恒成立; (3)当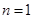 时,不等式显然成立; 当
时,不等式显然成立; 当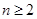 时,首先结合(1)中所求函数得出求和的表达式
时,首先结合(1)中所求函数得出求和的表达式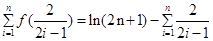 ,这样与所要证不等式较近了,再结合(2)中所证不等式,取
,这样与所要证不等式较近了,再结合(2)中所证不等式,取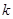 的最大值
的最大值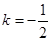 ,即
,即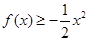 ,两式相结合,最后用放缩法可证得所要证明不等式.
,两式相结合,最后用放缩法可证得所要证明不等式.试题解析:(1)
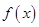 定义域为
定义域为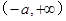
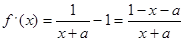 ,由
,由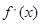 =0,得
=0,得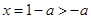 . 1分
. 1分当
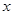 变化时,
变化时,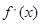 ,
,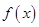 变化情况如下
变化情况如下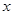 | (-a,1-a) | 1-a | (1-a,+∞) |
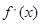 | + | 0 | - |
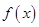 | 增 | 极大值 | 减 |
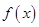 在
在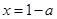 处取得最大值,故
处取得最大值,故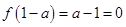 ,所以
,所以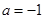 . 3分
. 3分(2)当
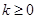 时,取
时,取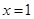 有
有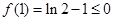 ,故
,故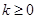 不合题意;当
不合题意;当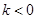 时,令
时,令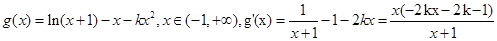 ,令
,令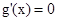 ,得
,得 ,①
,①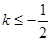 时,
时,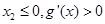 中
中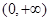 恒成立,因此
恒成立,因此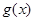 在
在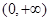 单调递增,从而对任意的
单调递增,从而对任意的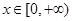 ,总有
,总有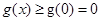 ,即
,即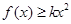 在
在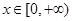 恒成立.故符合题意;②当
恒成立.故符合题意;②当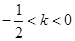 时,
时,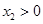 对于
对于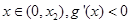 ,故
,故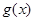 在
在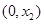 内单调递减,因此取
内单调递减,因此取 ,即
,即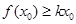 不成立,故
不成立,故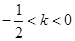 不合题意,综上,
不合题意,综上,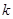 的最大值为
的最大值为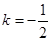 .
.(3)当
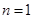 时,不等式左边
时,不等式左边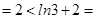 右边,不等式成立.
右边,不等式成立.当
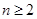 时,
时,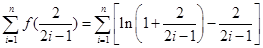
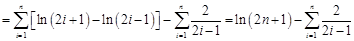 10分
10分在(2)中取

∴


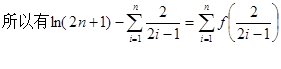 =
=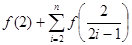
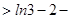
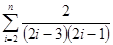
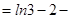
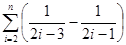
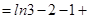
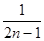
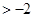 .
.综上,
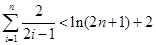
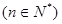 12分
12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
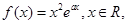 其中
其中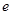 为自然对数的底数,
为自然对数的底数, 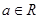 .
.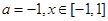 ,求函数
,求函数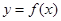 的最值;
的最值;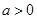 ,都有
,都有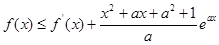 成立,求
成立,求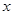 的取值范围.
的取值范围.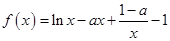 .
.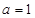 时,求曲线
时,求曲线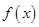 在
在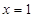 处的切线方程;
处的切线方程;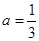 时,求函数
时,求函数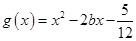 ,若对于
,若对于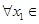 [1,2],
[1,2],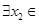 [0,1],使
[0,1],使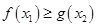 成立,求实数
成立,求实数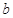 的取值范围.
的取值范围. ,恒过定点
,恒过定点 .
. ;
; 的图象向下平移1个单位,再向左平移
的图象向下平移1个单位,再向左平移 ,设函数
,设函数 ,直接写出
,直接写出 上的函数
上的函数 ,若在其定义域内,不等式
,若在其定义域内,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.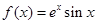 .
.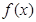 的单调区间;
的单调区间;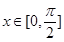 ,
,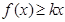 总成立,求实数
总成立,求实数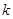 的取值范围.
的取值范围.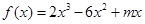
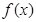 的解析表达式;
的解析表达式;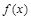 、
、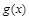 都是定义在R上的函数,
都是定义在R上的函数,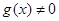 ,
,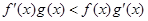 ,
,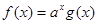 ,
,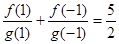 ,则关于
,则关于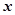 的方程
的方程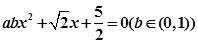 有两个不同实根的概率为( )
有两个不同实根的概率为( )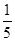
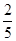
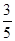
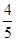
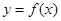 在区间
在区间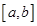 上存在
上存在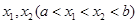 ,满足
,满足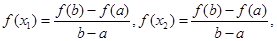 则称函数
则称函数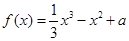 是区间
是区间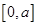 上的双中值函数,则实数
上的双中值函数,则实数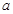 的取值范围是 ( )
的取值范围是 ( )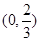
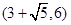
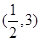
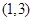
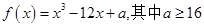 ,则下列说法正确的是( )
,则下列说法正确的是( )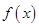 有且只有一个零点
有且只有一个零点