题目内容
6．判断方程x2+y2-4x+2y-1=0是否表示圆，如果是，指出圆心和半径．分析 分析：将圆的一般方程化成圆的标准方程，即可得到所求圆心坐标．解答：点评：
解答 解：将圆x2+y2-4x+2y-1=0化成标准方程，得（x-2）2+（y+1）2=6，
∴圆表示以C（2，-1）为圆心，半径r=$\sqrt{6}$的圆．
点评 本题考查了由圆的一般方程化圆的标准方程，利用圆的标准方程求圆心的坐标，属于基础题．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
11．在等比数列{an}中，a2=$\frac{1}{4}$，q=4，则a4与a8的等比中项是（ ）
| A． | 64 | B． | ±64 | C． | $\frac{1}{64}$ | D． | $±\frac{1}{64}$ |
1．
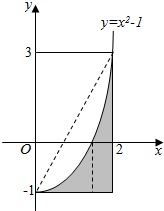如图，设区域D={（x，y）|0≤x≤2，-1≤y≤3}，在区域D内任取一点，则此点落在阴影区域M={（x，y）|0≤x≤2，-1≤y≤x2-1}内的概率为（ ）
如图，设区域D={（x，y）|0≤x≤2，-1≤y≤3}，在区域D内任取一点，则此点落在阴影区域M={（x，y）|0≤x≤2，-1≤y≤x2-1}内的概率为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{5}$ | D． | $\frac{3}{7}$ |