题目内容
1．
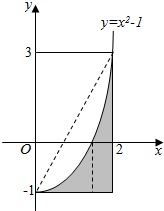如图，设区域D={（x，y）|0≤x≤2，-1≤y≤3}，在区域D内任取一点，则此点落在阴影区域M={（x，y）|0≤x≤2，-1≤y≤x2-1}内的概率为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{5}$ | D． | $\frac{3}{7}$ |
分析 先根据几何概型的意义，关键是要找出阴影部分的面积，及矩形的面积，再将它们代入几何概型计算公式计算出概率．
解答 解：将平面区域向上平移一个单位，
则阴影区域M={（x，y）|0≤x≤2，0≤y≤x2}
阴影部分面积S阴影=${∫}_{0}^{2}$（x2）dx=（$\frac{1}{3}$x3）|$\begin{array}{c}2\\ 0\end{array}\right.$=$\frac{8}{3}$，
矩形部分面积S矩形=（3+1）×2=8，
∴所投的点落在阴影部分的概率P=$\frac{\frac{8}{3}}{8}$=$\frac{1}{3}$，
故选：B．
点评 本题考查的知识点是几何概型概率计算公式，计算出满足条件和所有基本事件对应的几何量，是解答的关键，难度中档．
练习册系列答案
相关题目
6．已知P是△ABC所在平面内一点，4$\overrightarrow{PB}$+5$\overrightarrow{PC}$+3$\overrightarrow{PA}$=$\overrightarrow{0}$，现将一粒红豆随机撒在△ABC内，则红豆落在△PBC内的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{5}{12}$ | D． | $\frac{1}{2}$ |