题目内容
【题目】在直三棱柱ABC﹣A1B1C1中，D，E分别是BC，A1B1的中点．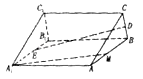 
（1）求证：DE∥平面ACC1A1；
（2）设M为AB上一点，且AM= 
AB，若直三棱柱ABC﹣A1B1C1的所有棱长均相等，求直线DE与直线A1M所成角的正切值．
【答案】
（1）证明：取AB中点N，连结EN，DN，
∵在△ABC中，N为AB中点，D为BC中点，
∴DN∥AC，
∵DN平面ACC1A1，AC平面ACC1A1，
∴DN∥平面ACC1A1，
∵在矩形ABB1A1中，N为AB中点，E为A1B1中点，
∴EN∥平面ACC1A1，
又DN平面DEN，EN平面DEN，
DN∩EN=N，∴平面DEN∥平面ACC1A1，
∵DE平面DEN，∴DE∥平面ACC1A1．
（2）解：作DP⊥AB于P，
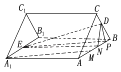
∵直三棱柱ABC﹣A1B1C1的所有棱长均相等，D为BC的中点，
∴DP⊥平面ABB1A1的所有棱长相等，D为BC的中点，
∴DP⊥平面ABB1A1，且PB= 
AB，又AM= AB，
∴MP= 
AB，
∵A1E=EP，A1M=EP，
∴∠DEP是直线DE与直线A1M所成角，
∴由DP⊥平面ABB1A1，EP平面ABB1A1，得DP⊥EP，
设直线三棱柱ABC﹣A1B1C1的棱长为a，
则在Rt△DPE中，DP= 
，EP=A1M= 
a，
∴tan∠DEP= 
= 
．
∴直线DE与直线A1M所成角的正切值为 ．
【解析】（1）取AB中点N，连结EN，DN，则DN∥AC，从而DN∥平面ACC1A1，再求出EN∥平面ACC1A1，从而平面DEN∥平面ACC1A1，由此能证明DE∥平面ACC1A1．（2）作DP⊥AB于P，推导出∠DEP是直线DE与直线A1M所成角，由此能求出直线DE与直线A1M所成角的正切值．
【考点精析】掌握直线与平面平行的判定和空间角的异面直线所成的角是解答本题的根本，需要知道平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；已知
为两异面直线，A，C与B，D分别是上的任意两点，所成的角为
，则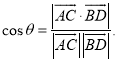
．
