题目内容
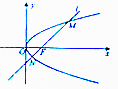
【题目】已知抛物线y2=2px(p>0)的焦点为F与椭圆C的一个焦点重合,且抛物线的准线与椭圆C相交于点 ![]() .
. 
(1)求抛物线的方程;
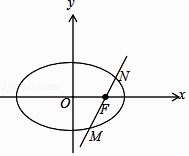
(2)过点F是否存在直线l与椭圆C交于M,N两点,且以MN为对角线的正方形的第三个顶点恰在y轴上?若存在,求出直线l的方程;若不存在,请说明理由.
【答案】
(1)解:由题意知, ![]() ,则p=2,
,则p=2,
∴抛物线方程为y2=4x
(2)解:设椭圆方程为 ![]() ,
,
则 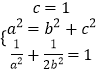 ,解得a2=2,b2=1.
,解得a2=2,b2=1.
∴椭圆C的方程为 ![]() .
.
若l垂直于x轴,得M(1,﹣ ![]() ),N(1,
),N(1, ![]() ),
), ![]() ,不符合;
,不符合;
若l不垂直于x轴,
设正方形第三个顶点坐标为P(0,y0),M(x1,y1),N(x2,y2)
令l:y=k(x﹣1)(k≠0),代入 ![]() ,得(1+2k2)x2﹣4k2x+2k2﹣2=0.
,得(1+2k2)x2﹣4k2x+2k2﹣2=0.
∴ ![]() ,
,
y1+y2=k(x1+x2)﹣2k= ![]() ,
,
则线段MN的中垂线方程为 ![]() ,
,
∴P(0, ![]() ).
).
由 ![]() ,得x1x2+(y1﹣y0)(y2﹣y0)=0.
,得x1x2+(y1﹣y0)(y2﹣y0)=0.
即 ![]() (y0≠0),∴
(y0≠0),∴ ![]() ,
,
又 ![]() ,∴
,∴ ![]() ,解得k=
,解得k= ![]() .
.
∴直线l的方程为 ![]() .
.
【解析】(1)由已知求得p,则抛物线方程可求;(2)设出椭圆方程,由已知列关于a,b,c的方程组,求得a,b的值,得到椭圆方程,当直线l的斜率不存在时,不合题意;当直线l的斜率存在时,设正方形第三个顶点坐标为P(0,y0),设出直线方程y=k(x﹣1)(k≠0),联立直线方程和椭圆方程,利用根与系数的关系结合 ![]() 求得k值.
求得k值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了促进学生的全面发展,郑州市某中学重视学生社团文化建设,现用分层抽样的方法从“话剧社”,“创客社”,“演讲社”三个金牌社团中抽取6人组成社团管理小组,有关数据见表(单位:人):
社团名称 | 成员人数 | 抽取人数 |
话剧社 | 50 | a |
创客社 | 150 | b |
演讲社 | 100 | c |
(1)求a,b,c的值;
(2)若从“话剧社”,“创客社”,“演讲社”已抽取的6人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.

