题目内容
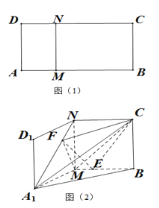
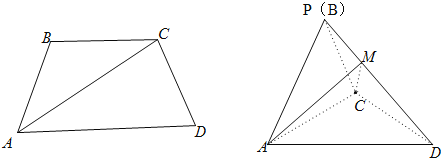
【题目】如图，在等腰梯形
中，
，
，现以
为折痕把
折起，使点
到达点
的位置，且
.
（1）证明：平面
平面
；
（2）若
为棱
上一点，且平面
分三棱锥
所得的上下两部分的体积比为
，求二面角
的余弦值.
【答案】（1）证明见解析；（2）
.
【解析】
（1）在梯形
中，取
的中点
，证明四边形
为平行四边形，再根据圆的性质得出
，利用面面垂直的判定定理证明即可；
（2）建立空间直角坐标系，由
得出
，利用向量法即可得出二面角
的余弦值.
（1）证明：在梯形中，取的中点，连接
则由
平行且等于
，知四边形为平行四边形
，由
，知
点在以为直径的圆上
又
，
，
平面
平面
又
平面
平面
平面.
（2）分别取
，的中点为
，
，连接
，
由
，可知
再由平面
平面
，为两平面的交线，
平面
平面
平面，
由于在
中，
，则
以为原点，
为
轴，为
轴，
为
轴建立直角坐标系
取
，则
，
，
，
由，得
设平面
的法向量为
；
则由
得
取
得
平面的法向量为
，
二面角为锐二面角，
其余弦值为.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】重庆市第八中学校为了解学生喜爱运动是否与性别有关，从全校学生中随机抽取50名学生进行问卷调查，得到如图所示的
列联表.
喜爱运动 | 不喜爱运动 | 合计 | |
男生 | 22 | 8 | 30 |
女生 | 8 | 12 | 20 |
合计 | 30 | 20 | 50 |
附：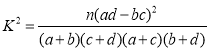
，
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（1）能否有97.5%以上的把握认为“喜爱运动”与“性别”有关；
（2）用分层抽样的方法从被调查的20名女生中抽取5名进行问卷调查，求抽取喜爱运动的女生、不喜爱运动的女生各有多少的人；
（3）在（2）抽取的女生中，随机选出2人进行座谈，求至少有1名是喜爱运动的女生的概率.
