题目内容
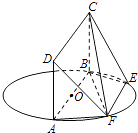
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D= ![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.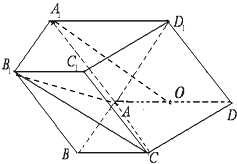
(Ⅰ)求证:A1O∥平面AB1C;
(Ⅱ)求锐二面角A﹣C1D1﹣C的余弦值.
【答案】(Ⅰ)证明:如图,连接CO,AC,
则四边形ABCO为正方形,
∴OC=AB=A1B1,且OC∥AB∥A1B1
∴四边形A1B1CO为平行四边形,
∴A1O∥B1C,
又∵A1O平面AB1C,B1C平面AB1C,
∴A1O∥平面AB1C.…
(Ⅱ)∵D1A=D1D,O为AD的中点,
∴D1O⊥AD,又侧面ADD1A1⊥底面ABCD,
∴D1O⊥底面ABCD,…
以O为原点,OC,OD,OD1所在直线分别为x轴,y轴,Z轴,
建立如图所示的坐标系,
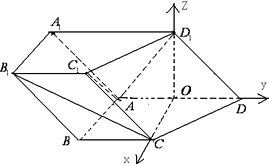
由题意得:C(1,0,0),D(0,1,0),
D1(0,0,1),A(0,﹣1,0),…
∴ ![]() ,
, ![]() =(0,﹣1,1),
=(0,﹣1,1),
![]() =(0,﹣1,﹣1),
=(0,﹣1,﹣1), ![]() =(1,﹣1,0),
=(1,﹣1,0),
设 ![]() 为平面CDD1C1的一个法向量,
为平面CDD1C1的一个法向量,
则 ![]() ,∴
,∴ ![]() ,
,
令Z=1,则y=1,x=1,∴ ![]() ,…
,…
设 ![]() 为平面AC1D1的一个法向量,
为平面AC1D1的一个法向量,
则 ![]() ,∴
,∴ ![]() ,令Z1=1,
,令Z1=1,
则y1=﹣1,x1=﹣1,∴ ![]() ,
,
∴ ![]() ,
,
∴所求锐二面角A﹣C1D1﹣C的余弦值为 ![]() .…
.…
【解析】(1)连接CO,AC易证![]() 为平行四边形,由此可证
为平行四边形,由此可证![]() ∥平面
∥平面![]() ;(2)以O为坐标原点,OC,OD,
;(2)以O为坐标原点,OC,OD,![]() 为x,y,z轴建立空间直角坐标系,利用法向量求出锐二面角。
为x,y,z轴建立空间直角坐标系,利用法向量求出锐二面角。
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.

练习册系列答案
相关题目